What is the Postgres' SQL GAME plan (I)?



Query optimization is not rocket science. When you flunk out of query optimization, we make you go build rockets. - Anonymous



    SQL 的 Query Optimization，被廣泛的認為( CMU/Andy Pavlo 、 Berkeley/Joe Hellerstein、UW-Madison/David DeWitt [1]* ) 是 Relational Database 實作中最困難的部分之一，本文從一個簡單的矩陣乘法問題出發，嘗試說明以下 Query Optiomization 的基本概念。

快速跳轉 🚀🚀🚀

為什麼 SQL 可以優化？ #

優化在 Computer Science 的世界裡面無所不見，舉凡

    上述的每一種優化都需要付出一些代價，代價指的是，因為獲得了效能上的提升，所以需處理一些因優化產生的問題，舉例來說





    SQL 不一樣，沒有優化器(Optimizer)，SQL 根本無法執行，這也是為什麼優化器常常跟計畫器(Planner)作為互相替代的詞，背後的原因就是強調 SQL 的 Declarative 性質，必須有一個 Optimizer/Planner 來產出可執行的計畫。

    用一個可能不那麽精準的比喻來類比優化器/計畫器在SQL中扮演的角色，你可以想像你是一家房地產建設公司，要開發一個新建案。



    SQL 作為一種 Declarative 的語言，只描述需要資料之性質，並不指定執行的過程。相信你可能看過這句話的各種版本，這到底是什麼意思？ Declarative 要跟 Imperative 放在一起比較才能看出區別，如果你手上有 DDIA [3]，趕快翻到第二章的資料查詢語言(query language for data)，我不可能寫的比 Martin Kleppmann 更好，其中 JS vs. CSS 是我看過最棒的例子。

    這裡我嘗試用 SQL VS. Dataframe API 的角度說明，Declarative(SQL) 跟 Imperative (Dataframe) 之間的差異是什麼？ 舉例來說，我想知道 NBA 西區球隊在 2021 年的平均薪資

Players #

idnameteamid
1L. James1
3C. Paul2
.......

Teams #

idnameconference
1LakersWESTERN
2SunsWESTERN
5NetsEASTERN
.......

Contracts #

idyearsalaryplayerid
12021411805441
22022444749881
32021353613602
........
SELECT   Teams.Name,
         Avg(Contracts.Salary::money::numeric::float8)
FROM     Players
JOIN     Teams ON  Players.teamId = Teams.Id  -- first join 
JOIN     Contracts ON Players.Id = Contracts.PlayerId -- second join 
WHERE    Teams.Conference = 'WESTERN' AND Contracts.Year = '2021'
GROUP BY Teams.Name

Dataframe(Pandas) #

# Ver 1 
( df_Players.merge(df_Teams,left_on='teamid', right_on='id',suffixes=("_player" , "_team"))
 .merge(df_Contracts,left_on='id_player', right_on='playerid')
 .loc[lambda row: row['year'] == 2021 ]
 .loc[lambda row: row['conference'] == 'WESTERN' ]
 .groupby('name_team')
 .aggregate({'salary':'mean'})
)

    看起來 SQL 跟 Dataframe 差異不大對吧？但我們用 Explain 解釋上面的 SQL，會得到一個 Plan ，也就是 SQL query 真正執行的方式，接著我們上下交換兩句 Join clause 的順序(first join、second join)，再用 Explain 解釋一次，你會得到一模一樣的 Plan 。會得到一模一樣的 Plan ，不是 Database 偷懶， 也不是 Plan 有 Cache(至少在這個例子不是)，而是因為，交換兩句 Join clause 在 SQL 的順序，並不會改變你想要資料的性質，所以 Plan 不會改變。

    其實，SQL 指定的資料性質不變，Plan 就不會改變。這句話是 錯的，錯在哪裡，後面的篇幅會解釋，我想強調的重點是。一樣的 SQL(每個字都一樣)，可能產生不一樣的 Plan ，不一樣的 SQL，可能產生相同的 Plan。

    是不是覺得有點混亂了🤔🤔🤔

    這邊我們先把視角放回 Dataframe，上面那個 Dataframe (Ver 1) 看起來很好啊，正確的回答了我們想要的資料。但其實這個 Dataframe 程式有一些優化的空間，比方說我們只想知道西區球隊的資料，所以可以在 Players 跟 Teams 的 Dataframe 合併後，就先把非西區球隊的資料挑出來丟掉，這樣非西區球隊的資料就不用再做一次跟 Contracts 的 Dataframe 合併運算，因為我們知道最後非西區球隊的資料在這個情境下根本用不到。

修改也很簡單

loc[lambda row: row['conference'] == 'WESTERN' ]

往上移兩行而已，這樣我們得到 Ver 2。

# Ver 2
( df_Players.merge(df_Teams,left_on='teamid', right_on='id',suffixes=("_player" , "_team"))
 .loc[lambda row: row['conference'] == 'WESTERN' ]
 .merge(df_Contracts,left_on='id_player', right_on='playerid')
 .loc[lambda row: row['year'] == 2021 ]
 .groupby('name_team')
 .aggregate({'salary':'mean'})
)

這時候一定有聰明同學想到，誒不是，那同樣的道理。我們是不是也可以在合併前就先把，非 2021 年的資料丟掉，恭喜，問了就有。

loc[lambda row: row['year'] == 2021 ]

移到 df_Contracts 旁邊。

# Ver 3
( df_Players.merge(df_Teams,left_on='teamid', right_on='id',suffixes=("_player" , "_team"))
 .loc[lambda row: row['conference'] == 'WESTERN' ]
 .merge(
     df_Contracts.loc[lambda row: row['year'] == 2021 ]
    ,left_on='id_player', right_on='playerid' )
 .groupby('name_team')
 .aggregate({'salary':'mean'})
)

   當然這邊還可以改進啦，把西區球隊在 Players 和 Teams 合併前就先挑出來，不過這不是重點。重點在於，你有沒有發現 Dataframe 跟 SQL 不一樣之處。我們怎麼寫 Dataframe，Dataframe 就會怎麼一行一行的執行，但我們怎麼寫 SQL，SQL 不一定照我們的寫法執行，這其中的差別正是 Declarative 跟 Imperative 的關鍵不同之處。

   在前面優化 Dataframe 的例子中，用的是一個在 SQL 中很經典的手法，叫做 Predicate Pushdown，核心的概念很簡單，如果查詢的結果不需要用到某些資料了，就早點把那些資料在計算的過程中丟了，以此降低 IO 與計算的成本，還有一個類似的概念叫做 Projection Pushdown，硬要區分兩者的差別，在於 Predicate 是減少 row 的數量，Projection 是減少 column 的數量，以前面的 NBA 西區球隊在 2021 年的平均薪資 來說，Predicate Pushdown 做的事情是把 Contracts 表中，非 2021 年的合約資料 (row) 先丟掉，Projection Pushdown 做的事情是把 Contracts 表中的 id 欄位 (column) 先丟掉*。都丟掉完再去做合併 (dataframe.merge or JOIN)，既不會影響最後的資料結果，又能達到降低 IO 與計算的成本。

*Projection Pushdown 在前面的 Dataframe 例子，我沒有做，但是可以做。

   現在你應該已經猜到，正是 SQL 的 Query Optimizer 在背後幫我們處理了 Predicate Pushdown 等繁複的工作，當年 Mike Stonebraker (2014 Turing Award) 跟 Jeff Dean (Google Senior Fellow & SVP) 關於 MapReduce 的大戰[4]，其中一個批評 MapReduce 的論點為，MapReduce 不是 Declarative 的語言，所以需要寫複雜的 map 還有 reduce 函式 ，就像回到 CODASYL 時代一樣(DDIA有介紹)。10 多年後來看，Mapreduce 確實某種程度上不再被 Google 所使用 [5]。

   David DeWitt 與 Mike Stonebraker 近年來的演講提到 MapReduce，都令我有種 真是
諷刺啊！紹安 的感覺(Stonebraker 70 & Stonebraker MSRA talk 2015)。但我認為兩方的衝突，是一個學術界跟業界觀點不同的好例子，學術圈講求的的是想法的突破，業界講求的是解決公司現有的問題。Google 三篇開創性的大數據論文，追求的其中之一是在大規模不可靠的硬體下，打造出夠可靠的軟體系統，因此公司可以買很多 CP 值高的硬體搭配 Linux ，來增加系統效能、容錯，不用去買 Sun 穩定高品質但價格昂貴的工作站。

   在那個當下，Google 沒有時間再花個好幾年，做出漂亮的底層系統(多年後，還是有了 Spanner ，Google 你是鬼吧)，因為每天使用者就是一直增加，數據更是指數型的成長。相反的學術圈的人就會覺得，要確定誒？ 這麼多資料庫的好東西，你們不用？ 我認為業界有著更明確的時間壓力，沒有辦法等到確定最佳解才開始動手，可是在那個當下不解決這個問題(Big Data)，很有可能就是公司失去競爭力。Joe Hellerstein (Berkeley CS Prof) 和 Doug Cutting(Founder of Hadoop) 關於此的討論具體，映射出了兩個陣營的觀點[6]。知乎上，马晓宇(PingCAP Director)的大數據與資料庫回顧也非常精彩 [7]。

Doug Cutting: "The interesting thing about MapReduce wasn't technical novelty but
practical utility. It wasn't hype. Folks used it to easily solve problems they couldn't before."

   回顧了一些歷史，我們發現到 SQL 相較與 DataFrame、ＭapReduce ，多引入了一層抽
象層，讓 “查詢” 跟 "執行/優化" 兩件事情分離，將繁瑣的優化任務交給優化器執行。

Pandas 作為資料科學中最被廣為使用的套件之一，當然有許多想改進 Pandas 的專案，那有沒有一種套件的 DataFrame 是像 SQL 一樣，會自動幫我們做些優化的呢？恭喜，問了就有。

   Polars [8] 諸多改進中包含 multi-threading、SIMD等，最令我覺得有趣的部分，即它引入一層抽象層，來處理前面提到過的 Predicate 和 Projection pushdown，讓使用者可以無痛的提升 DataFrame 的效能。所以說根據 Fundamental theorem of software engineering[9]，哪有加入一層抽象層不能解決的軟體工程問題？

   我認為這兩個問題，其實背後有相同的答案。因為 SQL 作為一種的抽象層，存在著大量
等價的具體可執行計畫，所以要由優化器在這大量計畫中，挑出盡可能好的一個計畫。

下一節我嘗試介紹大量等價的具體可執行計畫是什麼意思？這也正是優化器實作的主要困難之一。


[100 建中、雄女][中一中、中女中、鳳中、道明] #

設A=[12−323212]

試問 A192+3A45+2I=?

   希望這個標題跟題目，沒有讓你，終於想起被段考支配的恐懼，做為一直一來很經典的
矩陣單元段考考題，這類型有矩陣連乘的題目，解法不外乎就是。

甚至到了大學的演算法課、線性代數課，出了社會準備要刷題，矩陣連乘都沒有要放過你的意思，舉例來說台大的演算法課程，陳縕儂教授講解 DP(Dynamic Programming) 的其中一個例子，就是經典的 Matrix Chain Multiplication 問題，高中段考題想問的是一些特殊矩陣的性質。演算法課程著重的是用 DP 的方式，最小化一系列矩陣連乘的乘法次數，如下圖所示。

重點是 Matrix Chain Multiplication 這個問題，跟 Query Optimization 有什麼關係? 恭喜，問了就有。

    首先，我們先來理解這個問題，以上圖為例，4 個矩陣的連乘，我們發現有 5 種計算的方式，最後得到的矩陣結果會是一樣的，但是過程中需要耗費的計算資源會有相當程度上的不同，我們想要的就是最小化計算資源。

舉例來說
(((AB)C)D) vs. ((AB)(CD)) 就是 273 vs. 237 ，數字越小代表，需要的計算資源越
少，我們越喜歡這種順序。離散數學中的 Catalan Number(卡特蘭數) 在這裡可以派上用場，幫助我們得到矩陣個數與可行解數量的關係。假設矩陣個數為 n ，可行解數量就是 Catalan(n-1)。其實也很直觀，n 個矩陣相乘代表要找 n-1 個括號的合法順序。也可以代表 n-1 個非葉節點的二元樹數量。

Catalan Number 是一種指數型成長的函數，通常我們看到指數型成長，如果不是有關你的加密貨幣資產，那應該大事不妙。因為那代表問題計算起來很花時間，幸好在這個問題上至少存在一個時間複雜度為O(n3)的 DP 演算法。

繞了一小圈，有感受到一點大量等價的具體可執行計畫了嗎?

    Matrix Chain Multiplication 正是一個有大量等價解的問題，它的最佳解，只是給你一個藍圖，告訴你哪些矩陣先相乘，可以幫助你最小化計算資源。但在這指數成長的解空間中(大量)，每一個解，都會給你相同的結果(等價)，只是花的計算資源有高有低，這問題背後的結構跟 Query Optimization 基本上有 87% 像，這也是我會拿來類比的原因。

   到這裡我們可以嘗試簡單回答一下，在 Query Optimization 中所謂的 Plan 到底是什麼?
所謂的 Plan 就是一棵用二元樹表示的藍圖(基本情況上)*，代表著優化器的輸出，執行器的輸入，我們用 Explain 指令所看到的東西，優化器要做的事情就是在大量的 Plan 中挑出成本較低的一種 Plan。

優化器做的事情跟求 Matrix Chain Multiplication 的解非常像，如果你仔細看上面那張圖，會發現每一個 Matrix Chain Multiplication 的解都可以唯一的用一顆二元樹代表，找到 Matrix Chain Multiplication 的解不就是，找到一顆成本最小的二元樹。

*要是二元樹的Query Plan，代表所有 Plan 的 Operator 都是不超過二元的，除此之外 SIGMOD 21 有看到提議用 DAG 形狀的 Plan 的論文。

Matrix Chain Multiplication 問題可以幫助我們理解 Query Optimization 的不僅於此，找到此問題的最佳解，是一件事，做了這件事，我們已經花計算資源O(n3)，但還是沒有真的去把多個矩陣相乘的結果做出來，有沒有可能解 Matrix Chain Multiplication 根本不划算? 恭喜，問了，我也不知道？

我不知道現實世界中有沒有人會去解完 Matrix Chain Multiplication，再依此去做矩陣乘法，不過在 Query Optimization 的領域中，確實會發生，執行生出藍圖的步驟(Query Optimization)，花了太久的時間，以至於蓋房子(Query Excutor)的時候省下來的時間根本不划算，解決的方式也很簡單，不要規劃那麼久啊? 這是真的，後面的篇幅會再介紹。

此外，給定一種藍圖，我們可以對藍圖的每個部分採用不同工法，像是建案客廳的牆壁用實木貼皮，臥室的用刷漆。回到 Matrix Chain Multiplication 問題，以ABCD這四個矩陣相乘為例，有一種藍圖(可行的解)為((AB)(CD)) ， 我可以對這個藍圖，加上一些工法細節。

就算指定工法，藍圖還是只是藍圖，不過變成了有有工法的藍圖。

再以 Query Optimization 為例，優化器可以分階段產出 Query Plan

  1. 先產出沒有指定工法的藍圖，這種我們稱為 Logical Plan
  2. 再根據第一步產生出來的 Logical Plan ，生成 Physical Plan ，即有指定工法的藍圖

最後把 Physical Plan(有指定工法的藍圖)交給執行器(營建廠)

那有沒有一種藍圖，是只有部分節點有指定工法的？恭喜，問了就有，在優化器的優化過程中，即上面的步驟1跟步驟2中間，確實存在著一種 Plan，作為過渡產物，只有部分有工法細節的，也就是說它一部分是 Logical Plan，另一部分是 Physical Plan，但是，優化器再輸出給執行器前，必須把 Plan 的每個節點都轉成是有工法細節的，也就是說，輸出給執行器的一定是 Physical Plan 。

現在我們以一個更基本的視角來看待 Matrix Chain Multiplication 問題，它為什麼可以優化？答案非常簡單，因為矩陣乘法滿足結合律。以上圖來講那 5 個解均為等價，正是結合律的作用，完成所有乘法，最後得到的產物就會是相同的。

再想想前面提到的兩種 Pushdown 手法，為什麼可以 Pushdown ，因爲跟五洲製藥💊💊💊一樣，首先優化器有確定不傷身體(各個 Plan 結果會是等價的)，才講究效果(Plan 的成本)。換句話說沒有 Pushdown 跟有 Pushdown 的 Plan，交給執行器執行，都會是一樣結果，但是有 Pushdown 的 Plan 會執行的比較快，不傷身體永遠是第一考量。

更深層一點的說，是因為關係代數(Relational Algebra)良好優雅的抽象性，建立起那麼棒的抽象層，才使得優化器可以為了 SQL 的使用者，始終走在最前面。

到目前為止，我們都是以問題的角度來理解 Matrix Chain Multiplication 和 Query Optimization 之間的關係。我們試著以解法的角度來分析。非常推薦可以看完陳縕儂教授的講解，再回來閱讀接下來的部分。Matrix Chain Multiplication 的經典解法，用的是 Bottom-Up 的 DP。

我自己的理解，DP 的重點在於子問題的狀態，透過紀錄子問題的狀態與子問題解的對應，減少重複的計算。這個問題的狀態，是乘法開始的矩陣 與 乘法結束的矩陣，因為矩陣乘法不滿足交換律，所以矩陣之間的相對位置不會改變，用"開始的矩陣"跟"結束的矩陣"就可以表達狀態

舉 Matrix Chain Multiplication 例來說，LMNOPQR 七個矩陣相乘。
每一步我只想知道，是哪兩個(任何 n 個矩陣相乘，都可以看成 n-1 種兩個矩陣相乘)矩陣相乘會最小化成本。

假設做到最後一步，我知道是 (LMN)(OPQR)這樣會最小化成本，對於此時，我不在乎
(LMN) 子問題內部解，我也不在乎 (OPQR) 子問題內部解，我只在乎(LMN)的成本是
多少，(OPQR)的成本是多少，以及它們相乘的成本是多少。

LMN 問題的最佳解，可能是 ((LM)N)...
OPQR問題的最佳解，可能是 ((OP)(QR))、((O(PQ))R)...

但對 LMNOPQR 最後一步來說，他只想知道是不是 (LMN)(OPQR) ...
(LMN) 就是子問題的狀態，它隱藏了到底是哪一個解 ((LM)N)...
(OPQR)就是子問題的狀態，它隱藏了到底是哪一個解 ((OP)(QR))、((O(PQ))R)...

   Bottom-Up 的意思是，從大小較小的子問題開始計算，在這個問題上對應的就是，主對角線方向的填表方式。我認為理解 Matrix Chain Multiplication 的 Bottom-Up DP 會對理解 Query Optimization，非常有幫助，因為史上第一個 Cost-Based 的 Query Optimizer 也是採用了 Bottom-Up DP 的想法，Postgres的 Query Optimizer 也是從 Bottom-Up DP 作為核心開始一系列的優化。



IBM System R #

   IBM 的研究員 E.F. Codd 在 1970 發表了關係模型(Relational Model)，基於關係模型的資料庫，從此大大的改變了這個世界。但關係模型畢竟是一種概念上的指導，還是要有實際的產品來驗證概念，System R 和 Ingres 就是最早期，基於關係模型的關係型資料庫，兩者的良性競爭，大大地推進了資料庫領域的進步。兩者也在同一年獲得了 ACM Software System Award。

如果說 Google 的 GFS、Bigtable、MapReduce 開啟了大數據時代，我認為 IBM 毫無疑問一定是關係型資料庫的開創者，System R 幾乎有著現代資料庫的重要功能，包含了SQL、Transactions、Indexes、Cost-based Query Optimizer···

或者應該這樣說，現在的資料庫或多或少就是基於 System R 的技術上，其中最讓我驚訝的是 System R 的第一版竟然是 Columnar Store，我一直以為 Columnar Store 是比較後期的概念了。

   普遍公認 System R 是 Cost-based Query Optimizer(CBO) 的始祖，到底什麼 Cost-based Query Optimizer ? 為什麼前面要加一個 Cost-based ？ 顯然是有一種 Query Optimizer 做為 Cost-based 的對比。

沒錯，與 Cost-based 相對之就是 Rule-based Optimizer (RBO)，在 System R 劃時代的提出 Cost-based Query Optimizer 概念前，Query Optimizer 的實作基本上是 Rule-based ，或者說資料庫的實作，通常都是以 Rule-based 開始，因此你可以看到一些專案強調他們是 CBO，意思就是他們已經從 RBO 進化成CBO 。

Rule-based Query Optimizer 指的是 Heuristic (啟發式)的作法，依照經驗，做出自認為相對好的決定，比方說前面提到的 Pushdown 手法，因為優化器覺得 Pushdown 可能可以幫助我們降低計算量，所以先進行那些Predicate，但是這是優化器自以為的， Joe Hellerstein 有一篇論文就是在探討在有 UDF (user-defined functions) 情況下，Pushdown 不一定會是好的[10]。

或者回到矩陣乘法的那張圖，明明我舉的例子中，假如沒有方陣(行數等於列數的矩陣)，那張圖可以更看出可行解之間的成本差異，為什麼最後兩個矩陣，要用方陣？因為方陣有著許多特殊性質(旋轉、單位)，決定矩陣乘法連乘順序，當然也可以不用上面提到的經典 DP 演算法(Cost Baesd)， 我們可以採用一種啟發式規則(Rule Based)，盡可能讓會產生方陣的矩陣相乘，然後看看這些的方陣有沒有我們喜歡的性質，這些性質可以大幅降低計算量，像是單位矩陣，因為單位矩陣乘以任何矩陣，都會讓該矩陣不變。以上圖為例，會先處理最後兩個矩陣相乘(因為它們相乘會產生方陣)，再處理剛剛得到的方陣與大小7x3的矩陣相乘，最後把兩個剩下的矩陣相乘。

感覺到 Rule-based 與 Cost-based 的差別了嗎？ 一個是依照規則，機械的執行(Rule-based)，在執行規則的過程中不會去計算任何的參考數值。另一個會去計算出一個數字，代表解的品質，依此去解決問題(Cost-based)。

在開始介紹這 System R 前，先來談談我一直刻意忽略不談的一件事，Join，關聯式資料庫透過各式正規化，把資料分成一個一個的資料表，消除不必要重複，當有需求的時候再透過 Join 連接在一起。有一個冷笑話是這麼說的

Why do waiters hate DBAs?
Because the DBA always tries to join together two tables - Ryan Marcus

雖然有點冷，但是我認為展現出了關聯式資料庫對於 Join 的依賴。正規化 (Normalization) 的好處不僅於消除重複，很多時候冗余一時爽，資料亂葬場，不管是多核 CPU 的 Cache Coherence ，還是分散式系統 Cluster Replicate 的一致性，都是困難的問題，因為一旦一份資料有多個複製，就會產生一致性的難題(有些更新了，有些還沒)，Triton Ho 前輩曾寫了一篇，假如反正規化，可能會怎樣碰上 Race Condition 的麻煩，我認為是非常生動又清楚的說明。

我認為反正規化這件事情，有點像是對多個人說謊，因為某些方便，所以說謊，但卻要對多個人維持相同版本的故事，如果能維持的好，那當然沒問題，但是隨著時間拉長，可能早就忘記對誰說過謊了，更甚者，當另一個人要共同來圓謊的時候(接手的工程師)，不知道哪個才是真相。厲害的政治家當然有著厲害的說謊技巧，知道什麼可以說謊，知道說謊的代價自己付不付的起，而我認為反正規化，可能也是厲害的工程師需要的技巧，不過很多時候可能還是讓事情保持簡單，誠實為上。左耳朵耗子-陈皓 我做系统架构的一些原则，作為他20多年的開發經驗談，富有參考價值又有可操作性，其中第四條建議完备性会比性能更重要，即盡可能的維持關係型資料庫的正規化，再利用 NoSQL 作為補充。

除此之外，DDIA 第二章中，Bill Gates 履歷的那個例子，一份履歷假如一開始用 JSON 格式，可以運作良好，但是當想新增許多功能，而這些功能會需要多對多的參照時(學校的官網可能會變、推薦人的大頭貼可能會變)，就需要自己在程式端寫 Join 的邏輯。這時就需要考量 Schemaless 帶來的擴充性對比不需要額外維護 Join 程式碼邏輯的痛，到底想要哪一個。假如採用關係型資料庫，需要實作這種多對多的參照的功能，使用 Join 就非常方便，只是就需要好好思考 Schema 的設計。

如果你同意上述的好處，想必又加強了，想使用關聯式資料庫的動機，在使用聯式資料庫的情況下，勢必會用上 Join。對 Join 的處理，剛好為優化器最困難的部分之一。資料庫處理 Join 的困難之處有兩個，一個是 Join Algorithm，另一個是 Join Ordering，兩者我們都會討論到，不過我們先來粗淺的了解 Join Ordering，前面提到，優化器困難的原因之一是大量等價的執行計畫，你有沒有懷疑過，就做做 Pushdown 而已，哪裡來的大量等價執行計畫? 沒錯，之所以會有大量等價的執行計畫，其實是源於 Join 自身的性質。Join 運算子滿足交換律與結合律(Inner Join)。

說到這裡，你可能已經猜到了，Matrix Chain Multiplication 問題滿足結合律，搜尋空間就相當之大了，Join Ordering 又多了交換律 豈不是更大，恭喜，問了就是，目前你可以把 Join Ordering 想像成是 Matrix Chain Multiplication 問題，但是這只是一種類比，介紹完 System R 你會知道不同在什麼地方，但是整篇讀完後，我會告訴你相同在什麼地方。

前面提到的 Seletion、Projection、加上 Join ，就是傳統優化器聚焦的運算子，這三個合稱 SPJ 的組合，其各自的關係代數性質，造就了大量等價的執行計畫，我們再一次檢視

現實生活中，可以去做一件事，跟需要去做一件事通常無關，可以忠孝東路走九遍，不代表需要真的去走九遍。但現在，你應該更清楚的知道了 SQL 可以優化 跟 SQL 需要優化，其實是一體兩面，因為 SQL 可以看作是關係代數的一種包裝，關係代數的抽象能力，讓使用者非常方便的跟資料互動，然而怎麼真的存取資料這件事，還是需要處理，關係型資料庫把這件事交由優化器處理，優化器必須在大量等價的計畫中挑選出適當的計畫執行，所以非常困難。有多難？ 這裡就直接劇透了，NP-Hard。

介紹 System R 優化器前，先簡單介紹 Join 的原因是，第一讓大家更了解優化器的工作有什麼，第二解釋了傳統優化器中大量等價的執行計畫存在的原因，第三這樣才能解釋 System R 跟更早的資料模型有什麼差別? System R 優化器的論文名為 “Access path selection in a relational database management system”[13]，有意思的地方在於，Access path 恰好就是，關係模型的第一代競爭者，網路模型(Network Model)對於執行計畫的稱呼，我認為 System R 這篇論文就是想要主打網路模型的痛點，需要手動維護 Access path 。在 System R 中不管是單一資料表的存取方式，或是多表間的 Join 都無需使用者指定路徑，大大的降低了軟體應用的開發負擔。

關於網路模型可以參考 DDIA 的介紹。

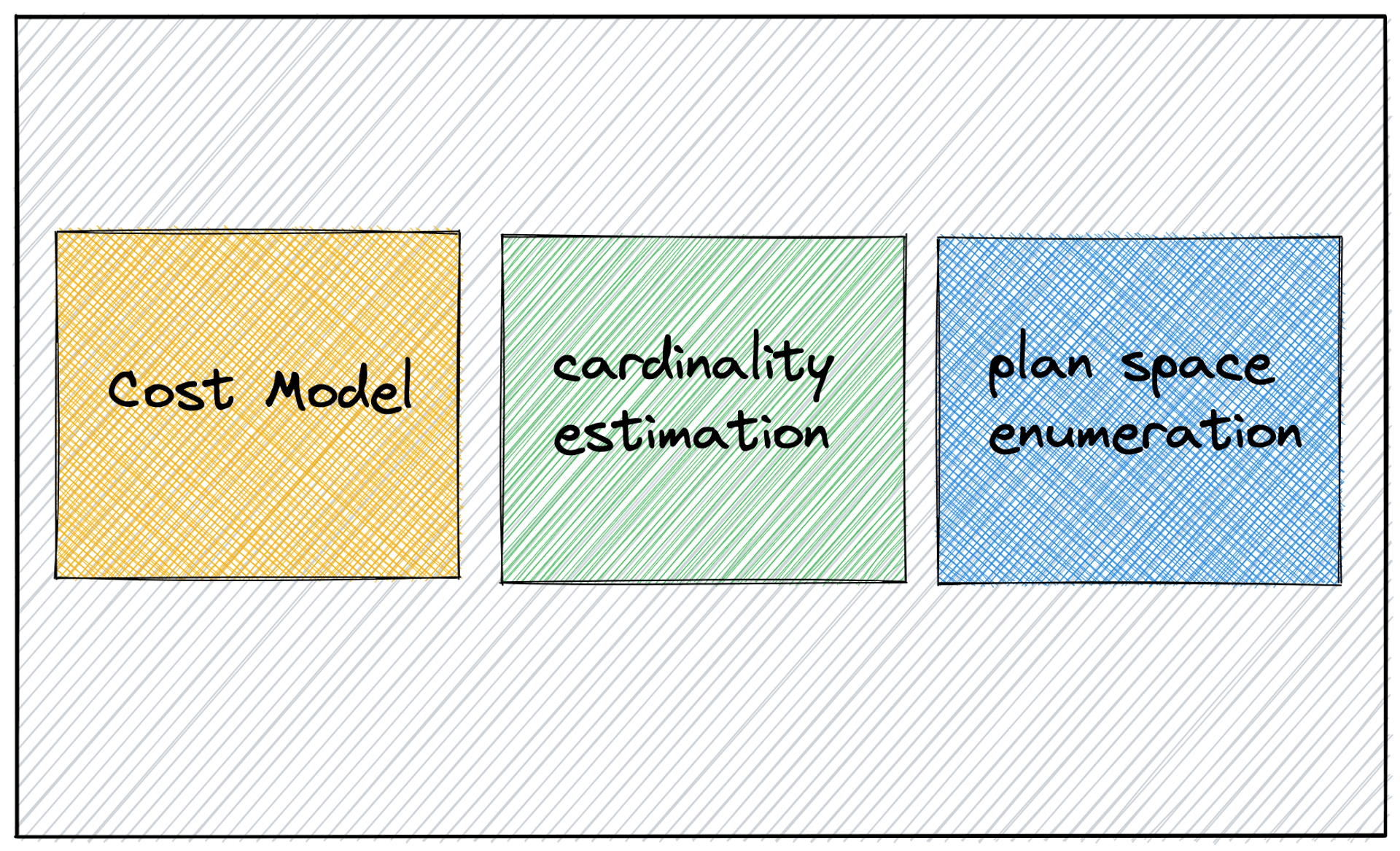
   一般來說，我們會將優化器看成是由三個單元的組成，上圖是後來的學者歸納出來的[11]，但這正是 System R 的三個大貢獻，有趣的事情是 System R 的優化器論文發表在 1979 的 SIGMOD 的 Database System Implementation 議程， 那也正是 David DeWitt 在資料庫領域的出道之作[12]，David DeWit 教授，除了學術上卓越的成就，一個很有名的事蹟是，Larry Ellison (Founder of Oracle) 曾經要求 UW-Madison CS 的系主任開除他，這件事後續影響了整個學術圈，形成了一個不成文的規定，我曾經寫過這件事，可以說是一個非常瞎的故事。

接下來我會依次介紹

接著在最後以這個架構，簡單解釋兩個真實的 Query Optimization 問題

Cost Model #

    優化器的功能就是挑出執行時間最少的 Plan，但優化器又不能真的去執行每一個大量等價的 Plan，顯然必須有一套估算的方式。就像是建築師畫出眾多符合業主需求的藍圖，並沒有建造實體的建物，他還是必須透過專業知識，判斷眾多藍圖的施工難度，此外假如有業主特別喜歡配合的營造廠，可能還要特別考慮進去該營造廠的獨門能力。優化器中的 Cost Model 就是估算 Plan 交給執行器執行的時間，估算執行時間這件事的困難之處在於。

  1. 執行同一種資料庫的機器非常多樣，有些電腦可能 CPU 運算能力強大，但記憶體較小，有些則反之，該資料庫優化器的 Cost Model 就必須盡可能辨別者兩種情況，這也是會有專家建議，假如你的機器是 SSD 的硬體配置，可以去調整某些參數，藉此加速效能，其背後的原理，就是透過提升 Cost Model 的精確度，加強優化器的決策品質，其中最有名的故事應該就是 Amplitude 透過調整一個參數，提昇一個查詢 50 倍，之後會再分析這個例子。

  2. 不同的資料庫，顯然會有不同的 Cost Model 考量，比方說分散式的資料庫，要考慮網路傳輸的成本，單機的 In-memory 資料庫不用考慮網路傳輸，但可能要考慮 Cache Miss 的次數，並沒有一個泛用的模型可以處理所有情境。

對於單機資料庫而言，IO 存取次數是 Cost Model 最重要的考量，既然 IO 存取次數最重要，那 IO 存取次數又相當程度上，取決於需要處理的資料大小，所以基本上 Coseted-based 優化器的 Cost Model 相當仰賴對要處理之資料大小的預測。

Cardinality Estimation #

   Cardinality 應該是從集合論來概念，在數學中指的是集合有多少元素，在這裡指的就是有多少 row 的資料，這也是 System R 的定義，即要處理之資料的大小，藉此來推估需要進行的 IO 存取次數，不過之所以要強調這是集合論來的觀念，是因為 Cardinality 在資料庫的脈絡中，有時候也會拿來當作有多少獨特的值(Number of Distinct Values)，因為集合不會有重複的元素，所以集合有多少元素，就代表有多少獨特的值。

你或許有聽說過，資料庫需要收集統計數據，來優化 SQL，指的就是 Cardinality Estimation 的基礎，對各個 Columns 的數據分佈計算(通常是 Histogram)，這部分詳細說明，可以參考清大吳尚鴻教授的資料庫系統概論，其中 Histogram 跟 System R 的 DP 我都覺得講的很清楚。

你可以大概想成是，假如現在有一個年齡 age 的 coulumn ，資料庫會收集 1~5 歲的有多少筆資料、5~10歲的有多少筆資料... 直到年齡的最大值，這樣遇到有 Query 用到 WHERE age = 8，就可以去5~10歲的統計數據那裡，大概猜出 8 歲的有多少筆資料。

我認為 Cardinality Estimation 不同於 CPU 的 Branch Prediction 和 V8 的 Speculative Optimization...，那些優化本質上是 Locality 的展現，Cardinality Estimation 要做的事情是 Data Sketching ，如同(Bloom Filter、Hyperloglog)，它想知道有某些特性的資料大概有多少筆。

有一類的問題，會給你一個 Query ，然後問你說哪一個 Index 最有效，舉例來說下圖是 Hussein Nasser 在他的 Youtube 頻道的問題

其實這類的問題，要碼是想問 Clustered Index 的特性，也就是資料表的 row 是按照 Clustered Index 的順序在硬碟中存放，假如用到 Clustered Index 做 Range Query 會因為 Locality 的關係，可能會特別快(推薦 CMU 的 Tree index slide)。或是 Covering Index 是什麼、或是 Multiple-Column Indexes 的 Match 順序。

要碼是真的想問哪一個 Query 比較快，如果是這樣的話，這不是一個好問題，原因是我們不知道 A、B、C 的數值分佈，也就沒有辦法做 Cardinality Estimation，更就沒辦法用 Cost Model 評估 Plan 的好壞。

這樣講可能有點抽象，我推薦兩個 Postgres 核心開發者的演講

  1. Explaining the Postgres Query Optimizer - Bruce Momjian [14]
  2. PostgreSQL Optimizer Methodology - Robert Haas [15]

Bruce Momjian 跟 Robert Haas 都是 Postgres 現今(2022)仍非常活躍的核心開發者，一個是 Core Team，一個是 Major Contributor，只想了解所謂 Cardinality Estimation 我會推薦第一個影片(Bruce Momjian)，第二個影片(Robert Haas)只有部分提到 Cardinality Estimation，但是都超級有趣，Robert Haas 比較著重在優化器的全局架構。

不，請千萬不要只看其中一個影片，兩個影片的觀念，都非常重要且實用，基本上是所有 Costed-Based 優化器共通的觀念，學一次可以用一輩子，超級划算。

透過他們的講解，你可以暸解

  1. 為什麼有時候建了 Index 還是沒有被使用?

    因為優化器根據 Cost Model 覺得用了會更慢。舉例來說，某個欄位的一種特定值佔比太多，你的 Predicate 又要挑這種特定值，那還不如直接 Sequential Scan 再濾掉不符合特定值的資料，因為 Index Scan 要用到多次 IO ，而且很有可能是隨機讀取(先不論 Bitmap Index Scan)，Sequential Scan 雖然是全部 row 都做一次，但是為順序讀取，順序讀取跟隨機讀取不管在 SSD 或是 HDD 都是順序讀取快很多，比例上來說，根據 Bruce Momjian 的說法，大約是超過 8% 的特定值資料，就會用 Sequential Scan。

    總結來說根據 Tom Lane(Postgres 中可能是最核心的開發者，你可以想成 Linus 之於 Linux) 的 Rule Of Thumb

    A rule of thumb is that plain index scan wins for fetching a small number of tuples, bitmap scan wins for a somewhat larger number of tuples, and seqscan wins if you're fetching a large percentage of the whole table

  2. ANALYZE(Postgres) 有多重要?
    沒有欄位的統計數據，優化器就只能用預設的值(selfuncs.h)，基本上效果不會太好。

  3. ANALYZE 所收集的數據，是關於資料的性質，基本上就是欄位之值的分佈，不是你跑的 SQL 所產生的任何數據，不是 Locality 的預測。

   如果你看完了 Bruce Momjian 與 Robert Haas 的講解還覺得意猶未盡，恭喜，我也是。所以我必須跟你推薦我最喜歡的資料庫文章作者 Justin Jaffray，Justin Jaffray 是前 Materialize 與 CockroachDB 的工程師，他寫的文章篇篇有趣，可以深入探討資料庫的一個面向，又講的非常清楚，配上乾淨的示意圖，對我非常有啟發，我這篇文章總共會引用他寫的三篇文章，第一篇是 Understanding Cost Models[16]，如果可以的話，我推薦的 Justin Jaffray 文章，都非常非常非常值得好好品味。

不管是 Robert Haas 在[15]覺得最麻煩的一個例子，或是 Justin Jaffray 在[16]中開頭的例子，還是Sam Wong 前輩的 trick，背後想傳達的意思就是，優化器往往很難在一個可以採用多個 Index 的 Query 中，挑到最好的那一個(先不論 Bitmap Index Scan)。

舉例來說

SELECT   *
FROM     Foo
WHERE    a = 1
ORDER BY b
LIMIT    10

假設 a、b 都有 Index，優化器到底要

如果 a = 1 的比例很低，顯然用 a 的 Index 比較好(只要讀很少的 row)，反之用 b 的 Index 比較好，從這個例子可以看出對於各個欄位資料性質的統計數據有多重要(預測 a = 1 有多少個 row 的誤差)，不過還有一種情況是統計數據非常準確，但是還是可能挑到錯的 Plan，像是 a = 1 的比例很高，但是大多數 a = 1 的 row ， b 的值都很大，那採用 b 的 Index ，可能不是一個好的 Plan (因為還是要讀很多不必要的 row )。

更要命的事情是，真實的 Plan 往往不是二選一這麼簡單，那有沒有什麼辦法可以讓我們了解到優化器到底面臨了什麼樣的難題，恭喜，問了就有，不管是 Justin Jaffray 在[16]，或者是 David DeWitt 在[12]，都放了一種圖，叫做 "Plan Diagram"，那正是 Guy Lohman (IBM DB2 Architect、2015 ICDE Chair)在[17]中提到他最喜歡的一篇論文之一 " Analyzing Plan Diagrams of Database Query Optimizers"[18]，這篇論文真的超級有趣，提供了非常好的視覺化方法，讓人能一目瞭然的理解，優化器在不同的數據下所決定最佳 Plan 。

此外這篇論文就是標準的 Dewitt Clause 案例，也就是我前面所說的，Larry Ellison 與 David DeWit 之間命運安排與情感的糾結，再次推薦我之前寫的文章，我一直跟我法律系的朋友推薦 Dewitt Clause 作為一個法律題目來研究，應該很有趣？ 可惜他們都不太喜歡，嚴格來說，Dewitt Clause 跟國會訂定的法律無關，所以應該不算言論自由(第一修正案)探討的範圍，但是我一個外行人的想法，還是覺得這個題目應該有研究的價值吧？

下面是 TPC-H 18 的 SQL 以及 Postgres 在這個 Query 的 Plan Diagram

select
  c_name, c_custkey, o_orderkey, o_orderdate,
  o_totalprice, sum(l_quantity)
from
  customer, orders, lineitem
where
  o_orderkey in (
    select l_orderkey from lineitem
    group by l_orderkey having sum(l_quantity) > 300
  )
  and c_custkey = o_custkey
  and o_orderkey = l_orderkey
group by
  c_name, c_custkey, o_orderkey, o_orderdate, o_totalprice
order by
  o_totalprice desc, o_orderdate;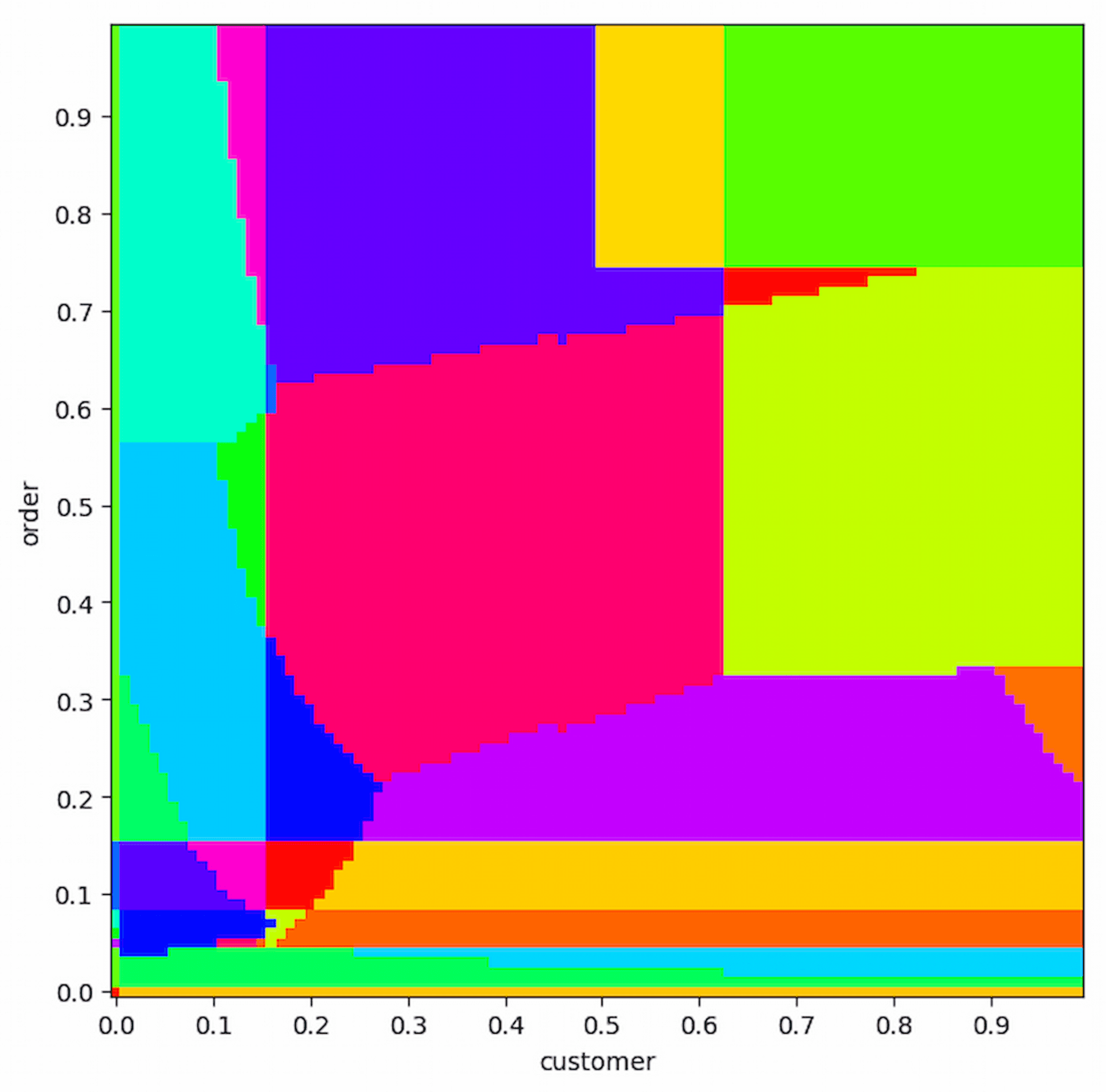

TPC-H-18 from Justin Jaffray
source: TPC-H-18 from Justin Jaffray

這種圖要呈現的資訊很簡單，每一種顏色，代表一種 Plan，之所以有那麼多顏色，就是代表在各種不同數據下，會有不同的 Plan，以上圖為例，，它是 Postgres 跑 TPC-H 18 的這個 Query 在不同的 order(Seletivity) 、 customer(Seletivity) 下，會選擇不同的 Plan。

這裡有一點值得注意的事情是，優化器在不同的數據下所決定最佳 Plan這句話，它可以代表

  1. 一模一樣(每個字都一樣)的SQL 因為數據的不同所以優化器採用不同的 Plan (可以參考[14]的 35:00 附近)，沿用[14]的例子，就是 WHERE letter = 'd' 這個 Query 現在跑，跟三個月後跑，會產生不一樣的 Plan(本來用 index ，後來可能不用了)，因為有新的資料的加入到資料表中，這解釋了前面的一個問題每個字都一樣 SQL，怎麼可能指定不同的資料性質？進而產生出不同的 Plan？，就是因為 SQL 確實沒變，但是資料表的數據變了，所以 Plan 要跟著變。不過假如都沒有新的資料加入，一模一樣的 SQL ，不管怎麼跑，Plan 都不會改變。

    其實仔細想想也很合理，WHERE letter = 'p' 因為一開始在資料表中佔了大部分的比例，所以採用 Sequential Scan，WHERE letter = 'd' 只佔一小部分，所以採用 Index Scan， 但很有可能隨著時間的變化，新的資料加入到資料表中，資料表中，變成 WHERE letter = 'd' 佔了大部分的比例，所以 WHERE letter = 'd' 要改用 Sequential Scan ， WHERE letter = 'p' 變成占比較少，要改用 Index Scan 。

    關鍵是有感受到優化器在背後又幫我們做了什麼了嗎？ 它時時刻刻注意統計數據的變化，這是假如你寫 Imperative 語言，可能需要自己去注意的，但是優化器幫我們做到了。優化器，你真厲害。

  2. 同一類 SQL 因為參數值不一樣產生不同的 Plan ，同一類的意思你可能猜到了，就是 Prepared Statement。

    所謂的 Prepared Statement 就是把參數模板化，Prepared Statement 把 WHERE letter = 'd' 或 WHERE letter = 'p' 改成是 WHERE letter = ?，在 Run Time 才知道 ? 是什麼值，它最廣為人知的功用，應該是預防 SQL Injection，但除此之外，它有一個效能上優點，從上面的例子中可以看出，因為統計數據的會隨著新加入的資料產生變化，所以即便是一模一樣的 Query ，仍然需要優化器重新規劃。

    但假如你的 Workload，資料隨時間的變化並不大，使用 Prepared Statement 讓你透過復用同一個 Plan，藉此省下重新規劃的時間。Prepared Statement 的重點，不只在於一模一樣 Query 可以省下重新規劃的時間，它是想要同一類的 Query 都復用同一種(或者說有限種) Plan，藉此省下重新規劃的時間，可是這會存在一個問題。

    沒錯，你可能猜到問題了， WHERE letter = 'p' 跟 WHERE letter = 'd' 可能數據分佈差距很大啊，這就是問題，通常來說 Prepared Statement 會使用 ? 的平均值來規劃 Plan。你現在知道了，有時候你覺得 Prepared Statement 很慢，可能就是使用與 ? 的平均值，差距很大的 Query，或是統計數據大幅改變，你需要重新規劃 Prepared Statement。

    這個問題非常重要，因為 Prepared Statement 在一般的 OLTP Workload 有很大量的使用情境， Guy Lohman 在[17]呼籲，資料庫學者該專攻的一個問題正是此，它有一個專業的術語叫做 Parametric Query Optimization，Andy Pavlo 對於 Prepared Statement 也有很棒的整理(2018 CMU 15-721 Optimizer Implementation Part I)。

    上面提到的 Plan Diagram(TPC H 18)，想描述的就是，就是這種情況，在講的更具體一點就是當我要撈的資料包括了

    • 50% 的 order 資料表跟 80% 的 customer 資料表 時，會是螢光綠的這種 Plan
    • 20% 的 order 資料表跟 50% 的 customer 資料表 時，會是紫色的這種 Plan
      ...

    一種顏色代表一種最佳 Plan，而這麼多顏色，優化器卻永遠挑 50% 的 order 資料表跟 50% 的 customer 資料表 桃紅色那種，顯然是會有點問題，目前也還沒有很好的解決方式。

    Cardinality Estimation 其實還有蠻多可以研究的，我上面只介紹我稍微了解的，其他像是 Deep Learning、Data Sketching、Sampling、、、 我完全不懂，但都是可以研究，非常有趣。但是我已經有點寫太長了，我們要進入所謂 System R 優化器的演算法啦！

Plan Space Enumeration #

   前面提到，Join 運算子符合結合律與交換律，因此存在了大量等價的 Plan(Join Ordering)，而我又介紹了 Matrix Chain Multiplication 問題，並且先催眠你把枚舉 Plan 的演算法想成就是，Matrix Chain Multiplication 的 Bottom-up DP 演算法，這邊請讓我再催眠你第二次，這次我們要先把 Join Ordering 想成另一個問題，然後再告訴你 System R 的演算法是什麼，之所以要這麼大費周章介紹兩個經典的演算法問題，請相信我絕對是有意義的。

講到一個 NP-hard 問題又有 Bottom-up DP 演算法，你會想到什麼？ 基本上我這種演算法麻瓜，只想得到 Travelling salesman problem(TSP, 旅行推銷員問題)，剛好這正是幫助我們理解 System R 的另一個經典問題。

TSP 描述起來簡單，但要找到最佳解，卻異常的困難，這裡我們直接開抄維基百科對 TSP 的定義，「給定一系列城市和每對城市之間的距離，求解訪問每一座城市一次並回到起始城市的最短迴路」，具體一點來說，現在有四個城市，起點是台北，其餘是匹茲堡、慕尼黑、阿姆斯特丹，總共會有 3! 種排列，因為起點跟終點要固定在台北。

台北 -> 匹茲堡 -> 阿姆斯特丹 -> 慕尼黑 -> 台北
台北 -> 阿姆斯特丹 -> 匹茲堡 -> 慕尼黑 -> 台北
台北 -> 慕尼黑 -> 阿姆斯特丹 -> 匹茲堡 -> 台北
.
.
.

前面我們不斷的強調大量等價的解，我認為在 TSP 也說得通，TSP 中的每一個解，保證一定旅行過所有城市剛好一次，但因為旅行的順序不同，造就了旅途的距離不同，或者我會這麼看待，上面的那個 -> 運算子，滿足交換律 。

TSP 的中的任何非起終點的城市，都可以跟以 -> 運算連接的城市交換，我再強調這是我自己的看法，很有可能是錯誤的，但我認為這樣想，對理解 Join Ordering 有幫助。

我們視覺化，台北、匹茲堡、慕尼黑、阿姆斯特丹的旅行順序，並且用二元樹的形式來表達，如下圖，每一種排列都對應一種左傾的二元樹，只是葉節點有排列的變化，左邊的數字代表旅行的距離，在這裡可以暫停一下，想一想這種二元樹跟 Matrix Chain Multiplication 的二元樹表示差異在哪裡？

TSP

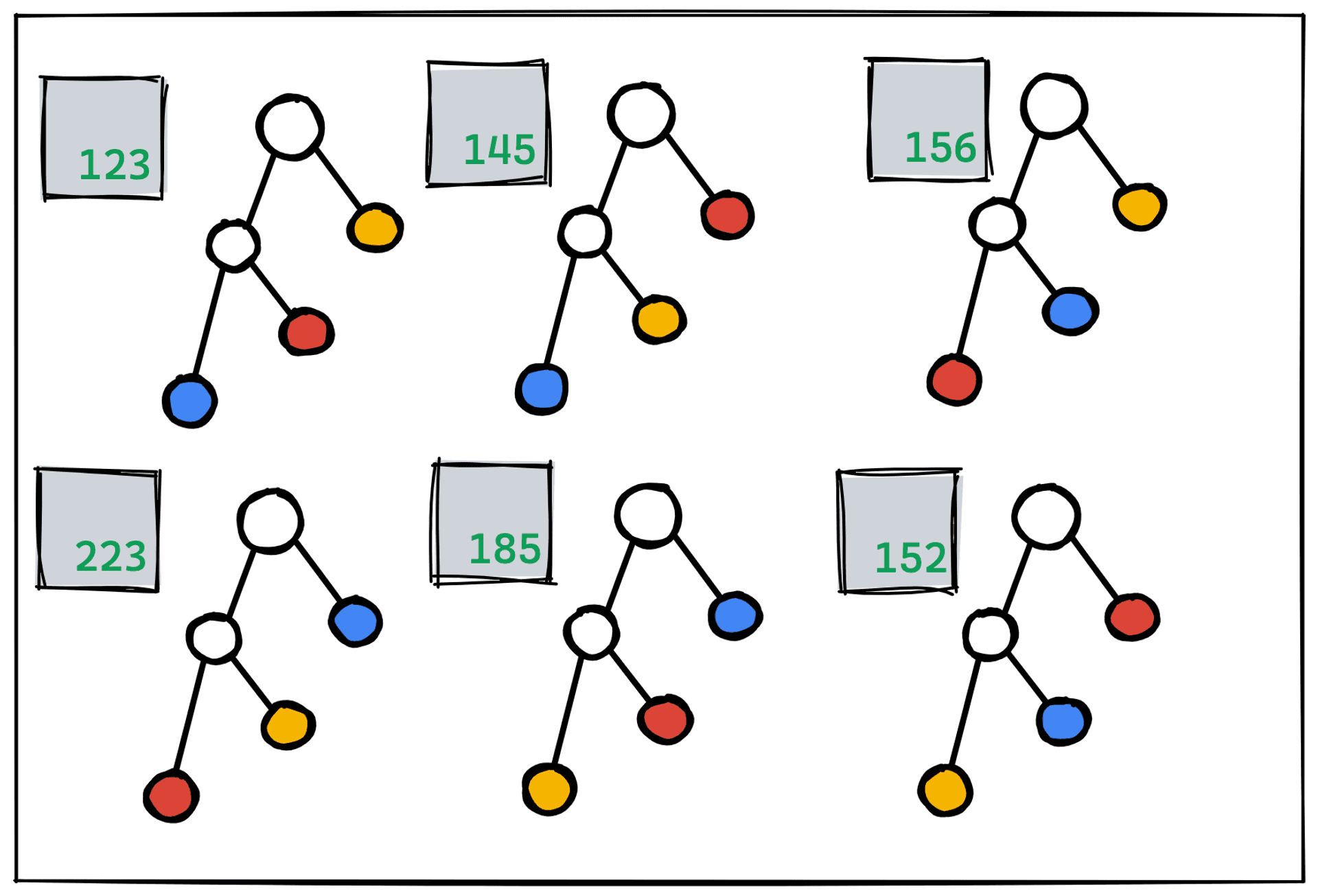
現在我們知道

並且針對上面三個問題的所有二元樹解，我們都可以算出它任一個子樹的數值(乘法次數、旅行距離、IO 成本)。

一如 Matrix Chain Multiplication，在以問題的角度介紹完後，改以解法的視角看待，我們來看看 TSP 的 DP 演算法是怎麼樣，這裡的演算法指的是 Held–Karp algorithm，Held-Karp 的狀態是 推銷員從起點出發已經旅行過 {B、W、D...} 這些城市，目前在 X 城市

舉例來說

台北 -> 匹茲堡 -> 阿姆斯特丹 -> 慕尼黑
台北 -> 阿姆斯特丹 -> 匹茲堡 -> 慕尼黑

在這個步驟中，我不在乎到底是先匹茲堡還是先阿姆斯特丹，我在乎的只是我已經旅行過{匹茲堡、阿姆斯特丹}，並且我現在在慕尼黑，還有這個狀態對應的最短路徑值。

{} 代表是集合，強調了並不在乎旅行過的城市的旅行順序
, 後面代表的是目前所在的城市。

Bottom-Up 的意思是，Held-Karp，會從旅行過的城市數較少的集合開始計算，演算法計算的順序如下

{},匹茲堡
{},阿姆斯特丹
{},慕尼黑

{匹茲堡},阿姆斯特丹
{匹茲堡},慕尼黑
{阿姆斯特丹},慕尼黑
{阿姆斯特丹},匹茲堡
{慕尼黑},阿姆斯特丹
{慕尼黑},匹茲堡

{匹茲堡、阿姆斯特丹},慕尼黑
{匹茲堡、慕尼黑},阿姆斯特丹
{阿姆斯特丹、慕尼黑},匹茲堡

{匹茲堡、阿姆斯特丹、慕尼黑}

Held-Karp 演算法，時間複雜度是O(n22n)，我自己的理解是共有n2n個狀態，每個狀態最多被分成 n 個子狀態的比較，如果了解了 Held-Karp，我認為就了解了 90 ％ 的 System R 的 DP 演算法。

System R 的 DP 演算法，並不打算處理 Join Ordering 的整個問題空間，它假設了兩個啟發式的規則，一個是只找 Left-Deep Tree 的 Plan，另一個是不考慮 Cross Product，我認為除了 Left-Deep Tree 可以節省記憶體使用量(Lin Ma 跟 Andy Pavlo 在 15-445 我記得都有提過)，還有另一個好處就是可以把 Join Ordering 當作 TSP 的變形來解(我自己的看法，很可能根本沒有這樣的意思)，等於說把結合律去掉，只解交換律產生的大量等價解空間。

把結合律去掉，只解交換律產生的大量等價解空間
把結合律去掉，只解交換律產生的大量等價解空間
把結合律去掉，只解交換律產生的大量等價解空間

System R 的 DP 演算法簡單來說可以看成，狀態是已 Join 過的資料表集合。舉例來說，假如有 R1、R2、R3、R4 四個資料表要 Join，演算法計算的順序如下

{R1}
{R2}
{R3}
{R4}

{R1、R2}
{R1、R3}
{R1、R4}
{R2、R3}
{R2、R4}
{R3、R4}

{R1、R2、R3}
{R1、R2、R4}
{R1、R3、R4}
{R2、R3、R4}

{R1、R2、R3、R4}

舉例來說，在 {R1、R2、R3、R4} 這步

最後挑出這4個中成本最小的一個順序。

System R 的優化器論文，並沒有給出詳細的複雜度(真是太無情了)，只有說大約是2n，但是在 “An Overview of Query Optimization in Relational Systems” 中[20] (應該是除了 System R Optimizer Paper 外，被引用最多次的優化器論文)，一筆劃的帶過，複雜度是O(n2n−1)，我當時候非常疑惑，覺得真的是哭啊，那個2n−1到底是？ 🤦‍♂️🤦‍♂️🤦‍♂️

後來我查了一下發現，Eric Brewer 對 Joe Hellerstein 筆記的講義複雜度也是寫O(n2n−1)，在那個當下我也還是沒有很懂，過了一個禮拜，我才完全搞懂，為什麼複雜度是那樣。

因為這個演算法的狀態是已 Join 過的資料表集合，每個狀態又會再分成，該狀態集合大小個子問題，所以複雜度才會是n2n−1，代表了，所有子集的大小加總(total sum of the sizes of the subsets)。

把 Held-Karp 演算法跟 System R DP 比較，你會發現，System R 的演算法只不過是狀態中少了一個，現在要 Join 的表，要不然推銷員從起點出發已經旅行過的城市集合 跟 ，已Join的資料表集合，基本是上是同一個想法。

可以再仔細看看，Held-Karp 的狀態後面有逗點，但是 System R 的狀態並沒有逗點。不過要理解這個演算法的全貌，還差一點點。

   vs.

Interesting order #

雜湊本無序，巢迴亦非第，合併無一律，排合蘊次順

請原諒我突然的詩句，因為我要介紹的是我最喜歡的 Justin Jaffray 文章，Merge Join is Weird，基本上 Join 的演算法並不難，透過討論三種最常見的 Join 演算法，你會明白

如果可以的話推薦先去看 Justin Jaffray 的文章，再接下去繼續閱讀，因為 Hash Join (雜湊合併) 與 Nested Loop (巢迴合併) 跟 Sorted Merge Join (排合合併) 本質上來說真的很不同。

Join 的本質是兩個資料表做 Cross Product，然後挑出符合 Pedicate 的 Row，我們就用最簡單的 Equal Join 為例子，用 Python 實作三個演算法。

TableA = [1,2,3,5,6,9]
TableB = [2,6,7,9,10,4]

一個最簡單的 Join 演算法，就是 Nested Loop Join，說穿了就是雙層 for 迴圈

def nestedLoopJoin(TableA,TableB):
    for rowA in TableA:
        for rowB in TableB:
            if rowA == rowB:
                yield (rowA, rowB)

Hash Join 演算法，先對一個 Table 建 Hash Table(Build Phase)，再用另一個 Table 找到對應的 Hash Table Slot(Probe Phase)

from collections import defaultdict
                
def hashJoin(TableA,TableB):
    hashTable =  defaultdict(list)
    
    for rowA in TableA:
            hashTable[rowA].append(rowA)
            
    for rowB in TableB:        
        for rowA in hashTable[rowB]:
            yield(rowA, rowB)

Sort Merge Join 演算法，先對兩個 Table 要 Join 的 Column 排序，最後跑一個類似 merge sort 演算法中 merge 的方法，merge 這步，只需要線性時間就可以完成。

def sortMergeJoin(TableA,TableB):
    TableA.sort()
    TableB.sort()

    pA = 0
    pB = 0
    pOrigin = None 

    while(1):
        while(pA < len(TableA) and pB < len(TableB) and TableA[pA] != TableB[pB]):
            if(TableA[pA] < TableB[pB]):
                pA+=1
            else:
                pB+=1

        if(pA == len(TableA) or pB == len(TableB)):
            break

        pOrigin = pB
        while(1):
            if TableA[pA] == TableB[pB] and pB < len(TableB):
                yield( TableA[pA] , TableB[pB] )
                pB+=1
            else:
                pB = pOrigin
                pA+=1
                break

Justin Jaffray 的文章要表達是，不管是 Nested Loop Join 或是 Hash Join，都有辦法用 Relational Algebra 表示，因為 SQL 可以說是一種 Set-Oriented 的代數 詳見 Pat Selinger 的這篇訪談，但 Sort Merge Join 完全沒辦法用關係代數(勉強可以用 Hash Join 的那個關係代數表示，Jens Dittrich 教授也有這種想法)，因為集合天生就沒有順序的概念，我非常同意 Justin Jaffray 的看法。

Interesting Order 的概念非常簡單，假設給你兩個已排序好的陣列，要你把它們 merge 起來，只要線性時間就可以辦到(Merge Sort 的 Merge)，推廣到全部解空間的枚舉上，就是 Interesting Order。

  1. 有三個資料表要 Join， R1、R2、R3，Join Predicate 是 R1.col = R2.col = R3.col，在 R1 Join R2 這一步用的是 Sort Merge Join，R3 又剛好 col 有建 Index，如此一來就像是合併兩個已經已經排序好的陣列，你只需要做 Merge 這一步。

    R1R2 Join R3 這步，會因為前幾步產生的"順序"，得到額外的加速，但是前幾步，可能因為要產生額外的 “順序“，付出了額外的代價，因此在 DP 的演算法中，必須考慮保留一些不佳的子問題解，因爲這個子問題解法，帶有額外的 “順序“，這種順序可以在更大的父問題中發揮加速的效果。

  2. 如果你看懂了 Interesting Order，可以再看一次 Merge Join is Weird，你會發現，順序在 Join 的演算法中確實是非常奇怪的，這可能就是那些 IBM 的大師，把有順序這件事，取名為 Interesting Order 。

  3. 除了多個表的 Join ，可以受益於 Interesting Order ， Order by 、 Group by 也都可能可以受益於 Interesting Order(如果做完 Sort Merge Join，剛好是 Order by、Group by 指定的順序)。

  4. Interesting Order 後來被推廣成 Physical properties，包含了資料是不是有按照某的欄位排序、按照分散式的機器分佈、按照某個 Hash 分佈... ， 或者你仔細想 Group By 根本不必到排序麽嚴格，只要資料都按照某個值分佈在一起就可以了...，諸如此類的資料特性，就稱為 Physical properties ，後面章節會再介紹，所以 Flink 中的 Interesting Properties 就是在描述這些事情( Physical properties )，在某些時刻資料有某種特性，在之後的時刻，這些特性可能會派上用場。

回頭再來看一次真正的 System R 演算法，如果只考慮 Logical Plan(只在乎多個 Join 之間的順序) ，確實就如同前面寫的那樣，是 Held-Karp 演算法的一種變形(我認為)，但事實上當年 System R 的整個 Join Ordering 是產出 Physical Plan 的演算法，也就是需要考慮到單表讀取要用哪個 Index、 多表 Join 之間的順序、每個 Join 要用什麼
Join 演算法(當年還沒有 Hash Join，所以就只要考慮 Nested Loop 跟 Sort Merge 兩個挑一個)，挑的方法很間單，Cost 最低的 Join 演算法一定會被保留，但是假如成本較高但是有產生 Interesting Order，那種 Join 演算法也會被保留。

關鍵就在於狀態會從

已 Join 過的資料表集合

變成

已 Join 過的資料表集合, Interesting Order

而 System R 中的Interesting Order 單純指的是對某個 Column 的順序，這個 Column 的順序要可以在 Order by、Group By、Join Predicate 中發揮加速的功用，特別一提 Join Predicate 中要做 Equivalence Class 推導。

真實 System R DP 演算法計算的狀態選擇如下。

-- 假設 
-- R2 的 colB、colH 有 Index 
-- R4 的 colB       有 Index 

WHERE 
R1.colA = R2.colB
R2.colB = R4.colB
R3.colx = R1.colx

Level 1

{R1}, Seq Scan
{R2}, Seq Scan (Cost 低)
{R2}, Index Scan on R2.ColB (Cost 高)
{R3}, Seq Scan
{R4}, Seq Scan (Cost 低)
{R4}, Index Scan on R4.ColB (Cost 高)

Level 2
{R1、R2}, Nested Loop Join no Interesting Order (Cost 最低)
{R1、R2}, Nested Loop Join Interesting Order (R1.ColA <=> R2.ColB) (Cost 最高)
{R1、R2}, Merge Join Interesting Order (R1.ColA <=> R2.ColB) (Cost 次低)

{R1、R3}, Nested Loop Join no Interesting Order

{R1、R4}, Nested Loop Join no Interesting Order(Cost 最低)
{R1、R4}, Nested Loop Join Interesting Order (R1.ColA <=> R4.ColB) (Cost 次低)
{R1、R4}, Merge Join Interesting order (R1.ColA <=> R4.ColB) (Cost 最高)

{R2、R4}, Nested Loop Join no Interesting Order
{R2、R4}, Merge Join Interesting order (R2.ColB <=> R4.ColB)

Level 3
{R1、R2、R3}, Nested Loop Join no Interesting Order
{R1、R2、R3}, Nested Loop Join Interesting Order (R1.ColA <=> R2.ColB)
{R1、R2、R3}, Merge Join Interesting order (R1.ColX <=> R3.colX)
{R1、R2、R3}, Merge Join Interesting order (R1.ColA <=> R2.ColB)

{R1、R2、R4}, Nested Loop Join no Interesting Order
{R1、R2、R4}, Nested Loop Join Interesting order (R1.ColA <=> R2.ColB <=> R4.ColB)
{R1、R2、R4}, Merge Join Interesting order (R1.ColA <=> R2.ColB <=> R4.ColB)

{R1、R3、R4}, Nested Loop Join no Interesting Order
{R1、R3、R4}, Nested Loop Join Interesting order(R1.ColA <=> R4.ColB)
{R1、R3、R4}, Merge Join Interesting order(R1.ColA <=> R4.ColB)
{R1、R3、R4}, Merge Join Interesting order(R1.ColX <=> R3.colX)

Level 4
{R1、R2、R3、R4},Merge Join ，Interesting order(R1.ColA <=> R2.ColB <=> R4.ColB)

最好的例子還是 System R Paper 後面的範例，尤其是論文中 Figure3、Figure4、Figure5、Figure6，實際上(Postgres)在處理 Intersting Order 的邏輯更複雜。但不管怎麼說，Postgres 的 Query Optimizer 就是標準的 System R Style， Postgres 的 Pathkey 就是 System R 中的 Intersting Order。



Amplitude 優化案例分析 #

    如果你看完了整個 System R 的優化器介紹，你一定會想知道了解優化器有什麼用？ 恭喜，問了就有，還有兩個。

這邊要特別強調一下，資料庫很慢，這背後可能有很複雜且多樣的成因，可能是 Connection 的問題、可能是你 work_mem 開太小的問題，可能是 WAL 的問題，關鍵是先確定是哪一種問題，非常推薦 Stephen Frost 的 Identifying Slow Queries and Fixing Them! 2021 PGCon NYC 的演講，講解了他認為常見的資料庫效能問題。

通常要到最後一步才是調整 Query Plan。

當我們真的要調整 Query Plan，一定要從前面的學過的知識出發，不然前面寫那麼多就太心酸了，我們知道優化器分成三個組成

所以 Query Plan 出了什麼問題，當然就是從這三個地方下手。

Amplitude 透過調整一個參數，提昇一個查詢 50 倍，Amplitude 是一間做網站數據分析的公司，我猜是更好用的 Google Analytics？

這個案例是講說，Amplitude 透過調了 Postgres 的 random_page_cost 參數讓某一個 Query 快了 50 倍，非常動人的調整，所以很多地方都有提過這個案例，因為這是所有工程師夢寐以求的情境吧(工程成本 vs. 獲得的收益)，但是老實說我看到簡介的第一個反應是，應該不是 random_page_cost 的關係。

原因很簡單，random_page_cost 影響的是 Cost Model，而 Cost Model 通常對 Query Plan 的影響不大，我舉兩個例子證明。

  1. 學術上以 " How Good Are Query Optimizers, Really? "[11] 這篇為代表，這是幾乎是近年討論 Query Optimizer 最常被提起跟引用論文(2015~2022 引用數已經 407)，裡面其中一個重要的結論是，讓 Cost Model 沒辦法分別好 Plan 跟壞 Plan 的原因，跟 Cardinality Estimation 相關性較大，Cost Model 本身的影響不那麼大。他們實驗的結果是，真實的 Query Runtime 和 他們的 Linear Model 的 差距最多就是 38%，我自己的解讀是，既然預測最佳 Plan 的 Cost 預測得很準，代表分辨好 Plan 跟壞 Plan的能力也很好，就代表不太可能挑到一個壞 Plan 比最好的 Plan 差了好幾倍。

  2. 實務上以 " Is Query Optimization a “Solved” Problem? "[17] 這篇為代表，Guy Lohman 是 IBM DB2 的主要設計者之一，他學術能力也很非常卓越，40 多年來他看過多少 Query，調過多少 Cost Model 一定比我們想的有料，他的經驗法則直接告訴我們，給定同一種 Cardinality，Cost Model 差不多是 30% 的誤差，我自己的解讀是，透過調 Cost Model，讓挑到 Plan 不一樣，不一樣的 Plan 間最多也就 30％ 的效能差別。

事實上我是對的。

Amplitude 的壞 Plan #


source: Amplitude

Amplitude 的好 Plan #


source: Amplitude

究竟 Amplitude 的 Slow Query 真正問題在哪裡？

我認為真正的問題是在於 Postgres 優化器的 hash join 實作沒辦法先把有用的 prop_keys 挑出來 (我認為這裡真正的問題是在於 Plan Enumeration)，證據是，壞 Plan 對 prop_keys 做了 seq scan。而且是一個 2千8百萬 row 的 seq scan，但事實上這 2千8百萬 row 有用的，只有 12萬多行，Hacker News 的第一則留言也是這種看法。

把 Hash Join 關掉，會有作用，是 Postgres 針對 Nested Loop Join，有一個特別的優化手段叫做 Parameterized Path，假如在沒有 Parameterized Path 的 Postgres 版本，我認為就算 Amplitude 也沒辦法重現把 Hash Join 關掉，用 Nested Loop Join 可以得到較好的 Plan 。

如果再仔細閱讀 Hacker News 的留言，你會發現一個有趣帳號 pgaddict， 如果我沒認錯的話，他就是 Tomas Vondra(Postgres 的 Major Contributor 之一)，Tomas Vondra 的點評也很直接

I don't know who recommends random_page_cost=1, but IMNSHO it's a bit silly. Even SSDs handle sequential I/O better than random I/O.

Values between 1.5 and 2.0 are more appropriate. I wouldn't really recommend 1.0 except when you know the data fits into RAM. There are other options that affect costs of random I/O,e.g. effective_cache_size.

所以別再相信，獅子的鬃毛式的參數調整，就可以把單一一個 Query 加速 50 倍，尤其是調整 random_page_cost 會影響到所有 Query，直接調成 1 真的不是一個好主意，但是假如你是用 SSD，把 random_page_cost 調的比預設的值 4 還要小，是合理的。

我認為在 Amplitude 的案例中，真正好的解法，是利用 CTE 或是 Subquery ，讓 Plan 不要去 Seq Scan prop_keys。此外，有一個 Domain Knowledge 是 Amplitude 文章沒有提到，但我猜測應該是存在的，也就是prop_keys 整個表中，專屬某個 app 的 row 應該是很少的，工程師該做的事情應該是充分利用這個 Domain Knowledge 去調整 SQL。

如果你看不懂我對 Domain Knowledge 猜測，推薦你閱讀 Spacelift 這篇，我認為可以學到更多東西，Spacelift 利用自身比 Database 多的 Domain Knowledge 來優化 Query，我認為這才是正規解法。



Dcard 優化案例分析 #

Dcard 的這篇技術分享，PostgreSQL 如何估算 HashAggregate 的 Return Rows ，以及低估的後果中，因為 CTE 缺乏統計資訊，所以優化器不知道有多少不重複的 user_id，只能採用預先寫死的 Magic Number 200，造成一個較慢的 Query Plan，解決辦法就是不要用缺乏統計資訊的 CTE，不管是問題還是解法，都寫的很精彩。

我個人認為，台灣公司的技術 Blog，Dcard 是寫得最好的之一，不管是遇到了什麼困難，怎麼解決，都在深度上還有重現性上，有很高的參考價值，也就是說你可以把他們的解法，用到自己的問題上。

我想對這篇精彩的文章，補充的東西是文章內提到的 Multivariate N-Distinct

Multivariate N-Distinct 是 Extended Statistics 的其中一種，所以容我把討論換成是 Extended Statistics ，Extended Statistics 就是來解決優化器實作中，對於 Predicate 間的獨立性假設與均勻性假設(其實主要是解決獨立性假設)。 這兩個假設正是 System R 當初開創的假設，舉兩個 Query 你就會懂獨立性假設了

獨立性假設，說的是現在有要找出 30 歲且身高 180 公分的民眾

SELECT name, id 
FROM  Citizen
WHERE Age = 30 AND  Height = 180

優化器最後估算結果的大小，就是用前面提到的 Histogram 去估算

  1. 看看 Age 的 Histogram 30歲的佔了多少比例(假設是 2.5%)
  2. 看看 Height 的 Histogram 180公分佔了多少比例(假設是 3%)

最後優化器就會假設這個 Query 撈出來的資料，佔了全部的 Citizen 0.75%，也就是把年齡跟身高當作是獨立事件，直接相乘。前面說過這是 System R 就開始延續下來的做法，各家資料庫基本上都還是沿用這個假設，但這會造成什麼問題 ?

SELECT name, id 
FROM  Citizen
WHERE BirthCity = '台北市' AND  BirthDistrict  = '大同區'

台灣只有台北市有大同區，所以也就是說只要是大同區出生的人，一定也是台北市出生的，但是在 Query 中還是會把他們當作是獨立事件。當 Predicate 一多的時候，獨立性的假設，就非常有可能產出非常不準的統計(Order Of Magnitude)，造成優化器挑不到好的 Plan。

均勻性假設假設，說的是一個 Column 的不同值，假設他們是均勻分佈，其實很簡單，舉例來說，就是假設

Age = 1 ~ Age = 100 每個值都一樣多，假如 Citizen 這個表有 30000 個 row，那因為 Age 有 100 個Distinct Values 所以 1 到 100 歲都各有 300 個值，顯然是會有點問題。

均勻性是 System R 一開始的假設，但是某種程度上已經透過 Histogram 修正了，不過當要用到多個 Columns 的時候Histogram 就派不上用場了。

為什麼會用到多個 Columns？ 答案就是在 Group By 的情境下，一次要 Group By 多個 Columns 是非常常見的，但是原本的 Histogram 幫不上忙，所以需要額外的統計數據，在沒有 Multivariate N-Distinct 的幫助下，預設的 Postgres 會假設多個 Columns 間是獨立的(又是你，獨立性假設)，直接把他們的 Number Of Distinct Value 相乘，相乘後的產物，當作是有多少 Groups 的預測，可以預見容易產生很差的統計數據，所以 Postgres 還有一個啟發式的規則，就是不管多個 Columns 怎麼樣乘， Groups 的數量不會超過該資料表的 10 %。

Extended Statistics其中的 Functional Dependencies 與 MCVs，就是專門來修正 Postgres 中對 WHERE Clause 的獨立性假設，Multivariate N-Distinct 是專門修正 Postgres 中 GROUP BY Clause 對獨立性的假設。Extended 的意思是相較原本的就有的 Statistics (Histogram)。

Extended Statistics 的 Commiter 正是前面提到的 Tomas Vondra， Tomas Vondra 在 2020 PGCON 的 CREATE STATISTICS - what is it for 演講，利用了英國的郵政資料作示範，獨立性的假設與均勻性假設會造成什麼問題，該怎麼透過 Postgres 的 CREATE STATISTICS 改進這類問題，進而讓優化器挑到好的 Plan，非常值得一看。

Postgres 的 Extended Statistics 現在還不能處理跨 Table 的統計數據，也就是說，假如你的有相關性的 Columns 是跨 Table 的， Extended Statistics 幫不到你，並且對非等於運算子，統計也不那麼準確，但我覺得 Tomas Vondra 考慮的蠻全面，把 CP 值夠高的 Extended Statistics 都做出來了，如果你發現你的 Query Plan 預估的 Cardinality 和真實的 Cardinality 差距過大，不妨想想看，是不是因為他們之間有統計上的相關性，Extended Statistics 或許幫的上忙。

關於獨立性假設，我最喜歡的故事是 Guy Lohman 在[17]寫到的 Redundant Predicates 案例，有一年他在美國的 IBM DB2 會議上，遇到了一位來自美國大型保險公司的女士，請教他一個 DB2 Query Optimization 的問題，問個問題還好，結果人家有備而來，竟然帶來了一疊 1 英吋厚的 Query Plans，由兩個非常相像的 Query 組成，要請 Guy Lohman 看看問題在哪裡，就在 Guy Lohman 壓力山大的時候，她說了一句:『 Query B 跟原本的 Query A 只多了一句 WHERE Predicate ，但是 Plan B 的執行時間慢了 Plan A 幾千倍』，剎那間 Guy Lohman 靈光一閃，他看了 Plan A 與 Plan B 的 Cardinality Estimation ，果不其然，兩者差了 10,000,000 倍。

Guy Lohman 繼續追問，多出來 WHERE Predicate 的 Column 是什麼？ 那位女士回答到，該 Column 是保險客戶 的 First Name + Middle Name + Last Name[:4] + ZIP Code + Social Security Number[-4:] 組合，你猜到了嗎？

Query Ａ 的其他 Predicate 包含了 First Name .. Social Security Number 這些 Column， 而 Query B 又多了那個組合碼的 Column，所以因為獨立性假設的關係。 💣 💣 💣， 直接讓 Cardinality Estimation 毀滅，Query B 多加的那個 Predicate 是完全沒幫助的 ，但原版的 DB2 優化器沒辦法識別這件事。 所以很多時候， Predicate 不是多就是好，必須要想想跟其他 Predicate 有沒有相關性。

透過 Amplitude 的案例，我們知道了調整 Cost Model 的幫助偏小，透過 Dcard 的例子，我們知道了一些改善 Cardinality Estimation 的方法。

Plan Space Enumeration 呢？ 基本上 Plan Space Enumeration 是不改資料庫的程式，你動不了的地方(Postgres)，所以說到底，改善 Query Plan 的方法只有，改善 Cardinality Estimation 嗎?

不，應該說 Plan Enumeration 枚舉不到最好的 Plan，但我們可以寫出想要的 Plan，我們才是資料的主人，資料有什麼特性，我們遠比資料庫知道，了解資料庫的侷限，就有可能結合資料庫跟資料的領域專業知識，創造出最好的 Plan。

寫出想要的 Plan，沒有什麼簡單的作法，我認為唯一的心法大概就是，知名 Scala 的專家李浩毅的心得

90% of my Postgres database optimization efforts are just splitting up big queries into smaller ones, suffering the additional round trips just so the query planner does the dumb/fast thing and doesn't do something superficially clever but ultimately counterproductive

我猜李浩毅的技巧應該就是用多個 CTE ，慢慢組出想要的 Query Plan，Bruce Momjian 在 CitusCon 2022 也有大略的提到這個技巧。

最後推薦大家可以從 Robert Haas 的個人網站，裡面有很豐富的材料，應該可以給你不少靈感，該怎麼調整你的 Query Plan。

菊下樓與 System R #

    System R 毫無疑問的是一個劃時代的產品，如果我們把 System R 比喻成菊下樓，Pat Selinger 就是當之無愧的阿貝師傅，System R 的優化器正是由 Pat Selinger 所設計，上面提到的所有有關 Postgres 的優化器主要想法，仍然不脫 1979 年 Pat Selinger 所提出來的概念，當然或多或少有一些變化。

David DeWitt 對 Pat Selinger 的評價是[21]

When you write one paper and that finishes off the field, that obviously is a superstar paper, and Pat is a true superstar!

Pat Selinger 的生涯在結束 System R 的研究後，就往管理軌走了，她當過 Jim Gray 的 Manager!!! 並且號稱可以讓 Jim Gray 做任何她想要他做的事情[22]。

System R 在開發的過程中，遇到了一個很有趣的 Bug，叫做 Halloween Problem，因為發生在萬聖節前夕，Don Chamberlin 叫大家先去放假，回來再處理，取個名字來方便討論這個 Bug，結果就叫做 Halloween Problem。

在萬聖節前夕， System R 上跑了一個 Query，對於所有薪資小於 25,000 的員工加薪 10%，但是到最後所有員工的薪水都超過 25,000了，怎麼會這樣 💸💸💸？

所有員工的薪水都超過 25,000，代表所有本來小於 25,000 的員工都被加薪至少一次，背後的原因，是員工這個表對薪資有建了 Index ，而優化器又利用這個 Index 快速的把薪資小於 25,000 挑出來，然後更新，但並沒有把更新過的 Row記下來，造成可能多次更新的情況。傳統的解決的辦法是，就是在有 DML 的情況下，會記住哪些是已經更新過的 Row。

Couchbase 有一篇解釋他們在分散式系統怎麼處理 Halloween Problem，我讀起來的關鍵是讓 Index 的讀與 Index 的更新，不要同步(Synchronously)進行？

如果有興趣的話程式設計大師智慧結晶：與主流程式語言的創始者對話，裡面關於 Don Chamberlin (SQL 的兩個發明者之一)的訪問有提到 Halloween Problem，一個訪問 IBM 眾多大師的文件裡，也有提到 Halloween Problem。

對於 Halloween Problem 還有一個更精妙的解法，就藏在下一段的 Exodus、Volcano、Cascades 的介紹，絕對會讓你 Ｏ口Ｏ ！！！



Exodus、Volcano、Cascades #

    介紹 Exodus、Volcano、Cascades 前，我們先來了解 System R 風格的優化器有什麼侷限？ 如此才能知道，Exodus、Volcano、Cascades 跟 System R 有什麼關鍵想法上的差別？ 解決了 System R 的什麼問題? 首先容我再說一次，System R 優化器是真正頂尖的研究，Postgres 至今(2022)仍然是一個標準的 System R 風格的優化器，但已經非常好用，解決了很多真實資料問題，是真正經的起時間考驗的想法。

我個人粗淺的看法是 System R 有 2 個大侷限跟 1 個小侷限

本文後續的篇幅，將會圍繞在 System R 後續的資料庫研究是怎麼攻克這 2 個大侷限跟 1 個小侷限。

Exodus 與他的繼承者們(Volcano、Cascades)，成功的解決了大侷限1，我認為其關鍵就在於 Exodus 的一個抽象手法。

    System R 的成功，無疑是開啟了資料庫的大航海時代，注意，我說的是資料庫，不是關係型資料庫，1980 年代關係型資料庫還未制霸整個資料庫世界(?)，有許多的資料模型(Data Model)被提出、研究、實作，像是 Daplex、ABE、GEM、GEMSTONE、IRIS，在這些研究中，很多工作是繁鎖且重複的[23]。

80 年代的 Exodus 就是在這樣的動機下誕生，Exodus 是一個完整的資料庫專案，由 UW-Madison 的 David DeWitt 與 Michael Carey 領軍，不過我們將專注在 Exodus 的優化器部份[23]，一個幫助大家打造自己的資料庫優化器的框架，我個人認為有點像優化器版的 Lex & Yacc。

假如你想打造自己的程式語言 ，一定想充分利用 LLVM 的工具鏈或是 Lex & Yacc，因為它們處理了一部分繁瑣的常見任務，以 Lex & Yacc 為例，你想要打造自己的編譯器，按照 Lex & Yacc 的語法定義出你的 Token 有哪些，文法是怎麼樣，就能生成你的編譯器(一個 C 語言的程式)。Exodus 也一樣，你定義好你的 Model Description File，優化器就可以由 Exodus 生成了。

看起來非常厲害，但 Exodus 怎麼辦到的(可以優化各種 Data Model)？ 或者該說 Exodus 做了什麼抽象化？



"Everything is a tree" #



我先強調，這是我一廂情願的看法，Exodus、Volcano、Cascades 原始文獻，並沒有出現過這句話，但是我會盡可能地說服你，為什麼 "Everything is a tree"，是我認為 Exodus、Volcano、Cascades 的核心想法之一。

   在 Unix 的設計哲學中，"Everything is a file"，如此的抽象化手法，統一了 Unix 所管理資源的介面，你可以一致的透過 Read、Write 等 System Call 存取 OS 管理的資源，像是 CPU 使用情況、Memory 使用情況 ...

在知乎上有一篇我認為很精彩的 "Everything is a file"討論 ，以下摘自該知乎問答

在 Linux 引入 signalfd 之前，signal 不是文件，你没办法用 poll 来等待 signal，只能用危险的 signal handler。 -- 陈硕

在 FreeBSD 引入 pdfork 之前，子进程不是文件，你没办法用 poll 来等待子进程退出，只能 wait。也没有办法安全（race-free）地 kill 进程。Linux 不支持 pdfork。[2020年补充：Linux 5.4 加入了 pidfd，也可以把进程当文件来等待 (poll)，但似乎还不支持线程] -- 陈硕

可以看出，駕馭 OS 這種大型軟體之複雜度的其中一個方法，是抽象出夠泛用的介面，並且盡可能的遵守介面的規範。

   在 Exodus 也是一樣的，"Everything is a tree"，如此的抽象化手法，統一了各個資料模型間的 Plan 介面，你可以一致的透過 Rule 對 Plan 做轉換，得到一個較好的 Plan。

真的是這樣嗎？ 我沒有超譯嗎？ 在 Exodus 優化器論文[23]中 Section 2 開頭，是這樣寫到的

In order to be sufficiently general, an optimizer generator must be based on an abstractlon of optimization suitable for most data models. We decided that queries and access plans should be expressed as trees, because we believe that operator trees are general to all set oriented data models in which complex queries are composed by nesting a finite set of procedures.

事實上我從本文的一開始，就一直不停的暗示"樹"這個概念在 Query Plan 的應用，Exodus 對於各種 set oriented 的資料模型，統一了其 Query Plan 的介面，就是一棵樹。

以 Exodus 的視角來看，Quyer Optimization 做的事情就是，在大量等價的樹中，找到成本最小的那一顆，前面提到的 Predicate Pushdown、Projection Pushdown、Join Ordering 通通可以看作是，由一棵樹 轉換成 另一顆樹，不用擔心後面會有視覺化的例子，本文的動畫預算都花在那個上面了，關鍵是使用 Rule 來進行樹的轉換。

這些樹，是一種資料庫要怎麼執行的藍圖，每一棵樹，代表一種藍圖，但是無論是這些藍圖哪一個被執行，得到的資料一定都會跟其他藍圖被執行，所得到的資料一樣，這正是我反覆強調的大量等價。

除了[23]的 Section 2，還有其它證據能證明 "Everything is a tree" 嗎？ 恭喜，問了有，我認為還有一項有力的證據就是，業界怎麼實作 Exodus 優化器 ?

不過，Exodus 只是學術上的一個原型，並沒有工業上的實作，真正在業界大放光彩的是 Volcano 與 Cascades ，而這三個優化器均是同一個人所創，他就是

(挪抬) Goetz Graefe。

你有看過 CMU Andy Pavlo 的 15-445、15-721 就應該有聽過的名字 Goetz Graefe，基本上大概每三四堂課，你就會發現，哇，Goetz Graefe 還有做這個喔！

Goetz Graefe 在 Linkedin 的自我介紹，是這樣寫的

Expert in entire database engines，確實。

根據 Stephan Ewen(Co-creator of Apache Flink) 所言，Flink 的 Hash join 和 Key-group partitioning 也受到了 Goetz Graefe 的影響

Goetz Graefe 在 2017 年獲得 SIGMOD Edgar F. Codd Innovations Award ， SIGMOD 每年只頒發給一位研究者的獎項，代表了獲獎者在資料庫上傑出的研究貢獻，獲獎的原因是

"for his foundational contributions to the architecture and implementation of database query optimizers"

Joe Hellerstein(Berkeley CS Prof) 表示

Winner of #SIGMOD17 Ted Codd Innovations award -- the big one

Apache Calcite 官方帳號 表示

Goetz Graefe invented the Volcano query planning algorithm, which is the heart of Calcite. He revolutionized databases.

Marcin Zukowski(Co-Founder of Snowflake ❄️) 表示

Happy to read Goetz Graefe won the SIGMOD Innovation Award. But now? He deserved it at least a decade ago already!


source: 火鳳燎原



Volcano Cascades 如何被實作的 ? #

    上圖這些軟體，其優化器背後用到的想法，都正是 Volcano 與 Cascades，讓我們先從 Apache Spark 開始，我第一次有好像知道 Volcano 與 Cascades 到底想做什麼的感覺(人生三大錯覺?)，就是看了 Michael Armbrust (Spark PMC) 講解他是怎麼設計 Catalyst，影片不長，12 分鐘左右，很值得一看。

Michael Armbrust 想表達的事情是，如果充分利用 Scala 的語言特性(Pattern Matching) 開發 Cascades 風格優化器，簡直不能再更快樂了。




為什麼 Pattern Matching，可以讓資料庫工程師的優化器開發非常順暢？


我認為，因為 Pattern Matching 很適合操作 Tree 這種資料結構。 Exodus 的第一版實作，正也是充分了利用 Pattern Matching 這個特性。

Goetz Graefe 在 Exodus [23]寫到

Ｗe initially intended to implement a rule-based optimizer using an AI lanuage like Prolog ... as those languages provide pattern matching and a search engine, and since unification can be used elegantly to build new query trees from old ones.

Exodus 的第一版優化器框架，是用 Prolog 這個語言打造的，Prolog 有著厲害的 Pattern Matching ，但後續因為效能的關係，改為用 C 語言實作。我當時的就有個猜想，“理解 Pattern Matching 很可能對理解 Cascades 風格的優化器有幫助”，因為

幸好 Python 3.10 引入了 Structural Pattern Matching，不然我是一句 Scala 都不會。一開始研究 Structural Pattern Matching 時，我也相當疑惑它跟 Switch 有什麼差別？ 推薦兩篇相當好的文章

看完了那兩篇精彩的介紹，我認為 Structural Pattern Matching 的 Or Pattern、As Pattern...等，確實比 Switch 靈活了很多，但 Goetz Graefe 還有 Michael Armbrust 應該不單是因為這樣，才做技術選擇的。一定是還有什麼我不夠了解 Structural Pattern Matching，因為我沒有看到 Structural Pattern Matching 跟 樹 的關聯。

如果再深入一點了，從 Python 的 PEP 635，可以看出，其 Structural Pattern Matching 是取逕於 Haskell、Erlang、Scala 等函數型語言，所以試著寫一下 Python 的 Structural Pattern Matching，應該確實對感受其他語言的 Pattern Matching 有幫助？ 以 PEP 635 的第 2 個程式範例來說

沒有 Structural Pattern Matching 前，要分析 AST 有沒有特定的 Pattern，
像是 A + B * C，需要這樣寫

if (isinstance(node, BinOp) and node.op == "+"
        and isinstance(node.right, BinOp) and node.right.op == "*"):
    a, b, c = node.left, node.right.left, node.right.right

有了 Structural Pattern Matching，只需要

match node:
    case BinOp("+", a, BinOp("*", b, c)):

只需要想著，我要 Match 的資料形狀，那些繁瑣型別判定，Python 的 Structural Pattern Matching，在背後通通幫我們做掉了，更棒的是，Match 到的 a b c 值，已經幫我綁定好了(PEP 中有強調是 bind 不是 assign，我猜是因為 bind 代表著，做了更少次的記憶體操作)，在接下來的程式可以直接使用這些值(需要小心 Shadowing)。

當初發現 PEP 635 那個範例，我大概就知道，中大獎了！ 那個感覺就像，點進去 Stack Overflow，看到你要問的問題有一個 300 likes 的答案，或是答案裡面有跟你的問題，一模一樣的關鍵字。

PEP 635 的 Rationale 開宗明義地寫到

Much of the power of pattern matching comes from the nesting of subpatterns. That the success of a pattern match depends directly on the success of subpattern is thus a cornerstone of the design.

Pattern matching 強大的地方，在於可以 Match Nesting of Subpatterns，至於最常見的巢狀資料之一是什麼？我想樹就是一個常見的例子。

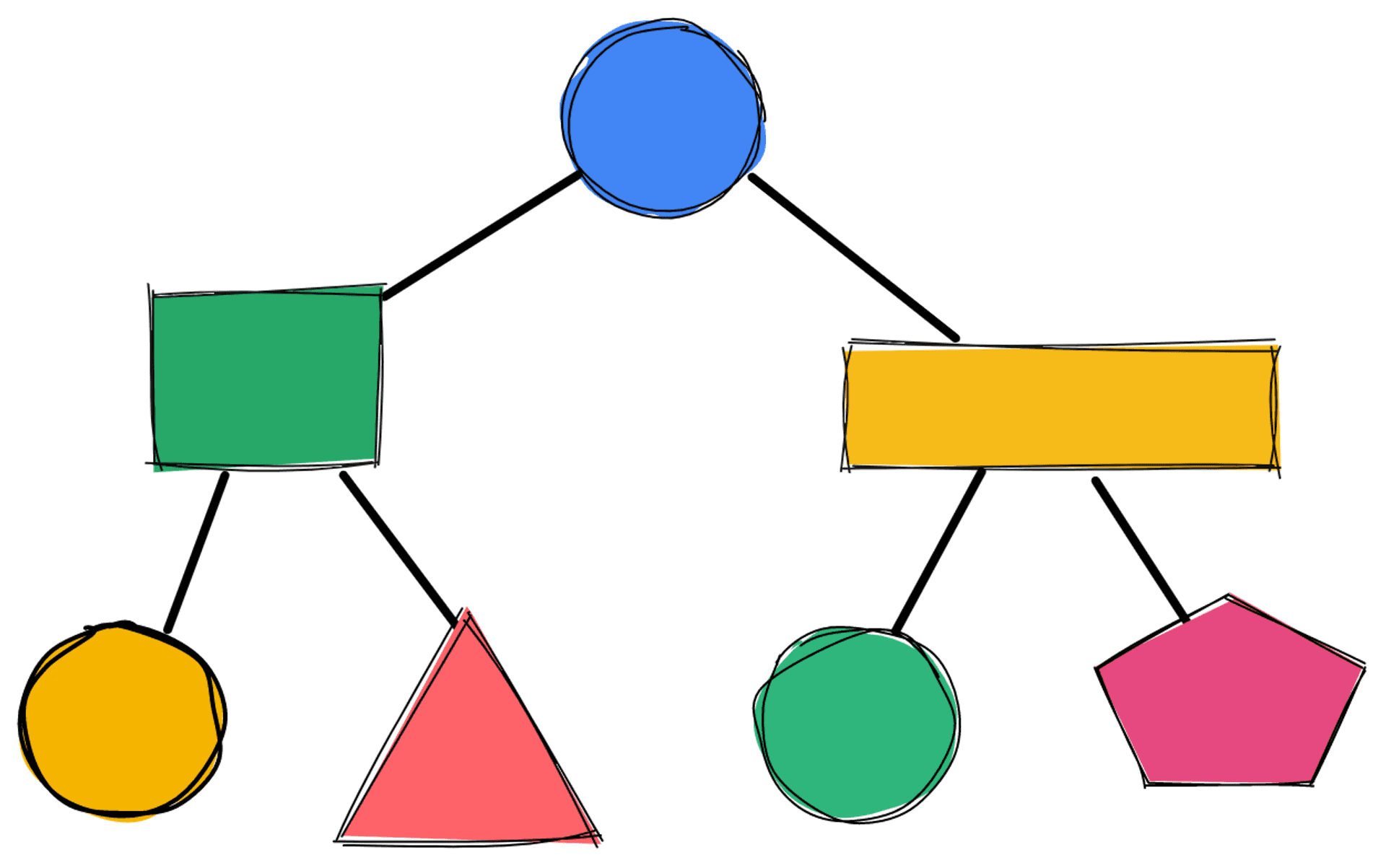
假設現在我要在一種有各種顏色形狀的二元樹上，找到一些 Pattern。

給定一顆這種樹，我想知道

  1. 樹上有沒有綠色的正方形，左邊的節點連著紅色圓形
  2. 樹上有沒有任何顏色任何形狀，左邊的節點連著黃色三角形，右邊的節點連著藍色長方形
  3. 樹上有沒有黃色的圓形，左邊的節點連著藍色長方形，該藍色長方形，左邊的節點連著紅色三角形，右邊的節點連著紅色長方形，該紅色長方形，右邊的節點連著綠色正方形

我腦海裡會這樣想

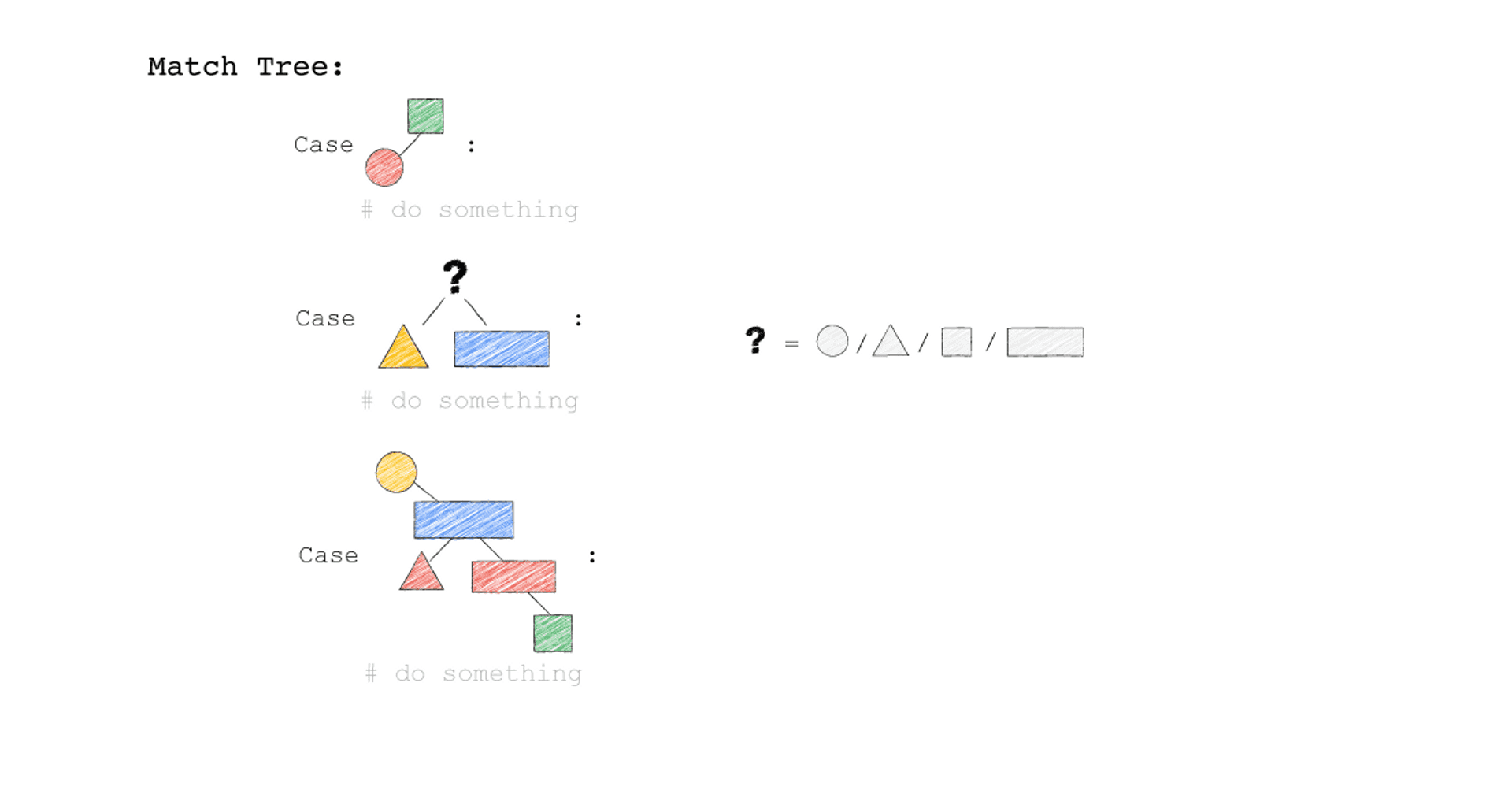
精彩的地方來了，你程式確實就這樣寫就好

def Find(Tree):
  match Tree:
    case Square('green' , 
            Circle('red') as left , 
            _
          ) as root:
            print(f'case1 \n  {root = } \n {left = } \n ')
      
    case Geometric( _ , 
              Triangle('yellow') as left,
              Rectangle('blue')  as right,
            ):
            print(f'case2 \n {left = } \n {right = } \n')

    case Circle('yellow', 
             _ ,
             Rectangle('blue',
                Triangle('red'),
                Rectangle('red',
                    _ ,
                    Square('green')
                ),
             ) as right
          ) as root:
            print(f'case3 \n {root = } \n {right = } \n ')
            
    case _:
            print('Not Found \n')

完整版的程式

完整版程式，可以更深入探討以下問題 （要在 Python 3.10 以上的環境）

  1. 不同形狀的 Geometric_tree ，丟進去 Find 函式 會發生什麼事?
  2. 為什麼 Geometric_tree2 不會 match，Geometric_tree2.left 卻會 match ?
  3. Geometric_tree3 跟 Fruit_tree1 的差別 ?
  4. 已經 Bind 好的 left 、 right 你可以秀什麼操作 ?

關鍵在於，我腦海中想像 "樹" 的形狀，可以非常輕鬆的轉成程式碼，重點不單在圖，也不單在程式碼。重點在，腦海中的圖到程式，轉換的過程是很直覺的，直覺到，我認為只要有一張二元樹的圖，任何一個高中生(不用日本的)，都能簡單利用 Structural Pattern Matching ，把在二元樹上找到某個類型的 Pattern 這件事，俐落的完成。

    上面那個小實驗，想表達的是，Pattern Matching 確實是操控樹這種類型資料結構的優雅方法，不過"Everything is a tree"，還沒解釋清楚，容我再重複一次。

在 Unix 的設計哲學中，"Everything is a file"，如此的抽象化手法，統一了 Unix 所管理資源的介面，你可以一致的透過 Read、Write 等 System Call 存取 OS 管理的資源，像是 CPU 使用情況、Memory 使用情況 ...



在 Exodus，"Everything is a tree"，如此的抽象化手法，統一了各個資料模型間的 Plan 介面，你可以一致的透過 Rule 對 Plan 做轉換，得到一個較好的 Plan。(再次強調，這是我的腦補，原始論文並沒有這句話，我有超譯的可能)

我沒解釋清楚的部分是 Rule，我認為，每一個 Rule 只需由 2 個動作組成

  1. Match (Antecedent, ”before” pattern)，代表原本的樹有沒有出現 "某種 Pattern"

  2. Substitute (Consequent, ”after”-pattern)，要轉換成"哪一種 Pattern"(前提是 Match 成功)

*Match 是 Exodus 的術語，Substitute 是 Cascades 的術語，方便解釋，我這裡混用。

以 "Everything is a tree" 的視角來看待 Query Optimization， 所有的 Query Plan 都是一棵樹，樹與樹是等價的，我們從一顆原始的樹開始，利用互相獨立的 Rules，慢慢把那顆原始的樹，一生二，二生三，三生萬樹，在所有樹構成的森林中，找到成本最小的樹

給定一種 Rule 就是給定一種，把原本的樹，轉成新的樹的方法，視覺化整個 Query Optimization 的過程(Exodus 的視角) ，就是如下三個動畫，建議先不要看圖片的解說文字，先看一下三個動畫，感受動畫到底想表達什麼 ?

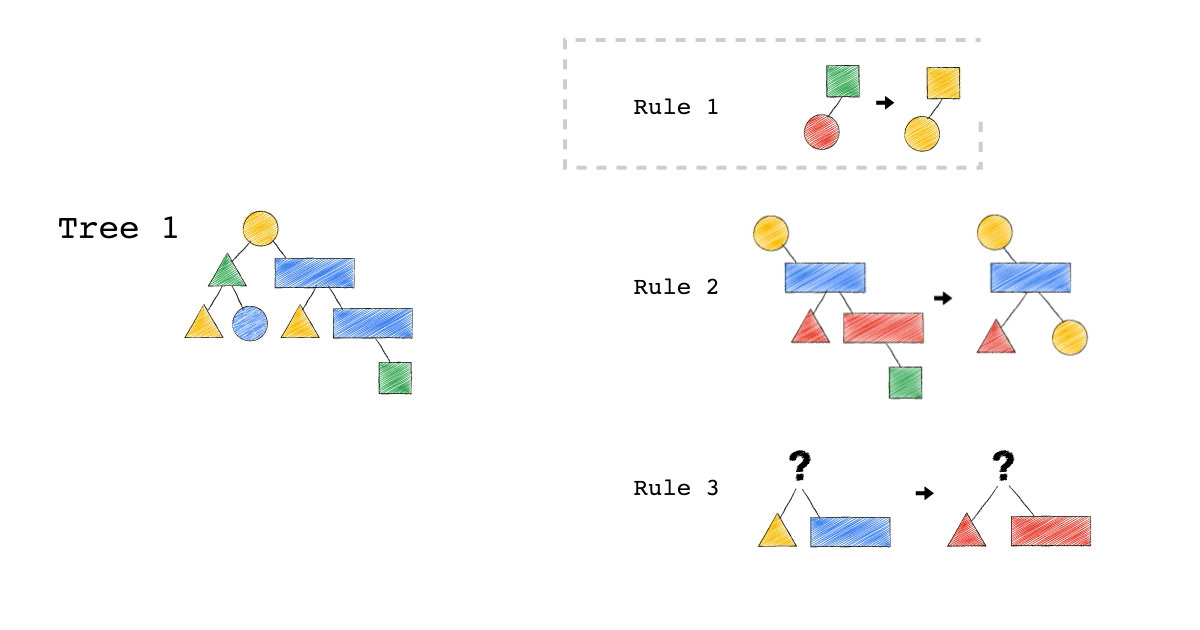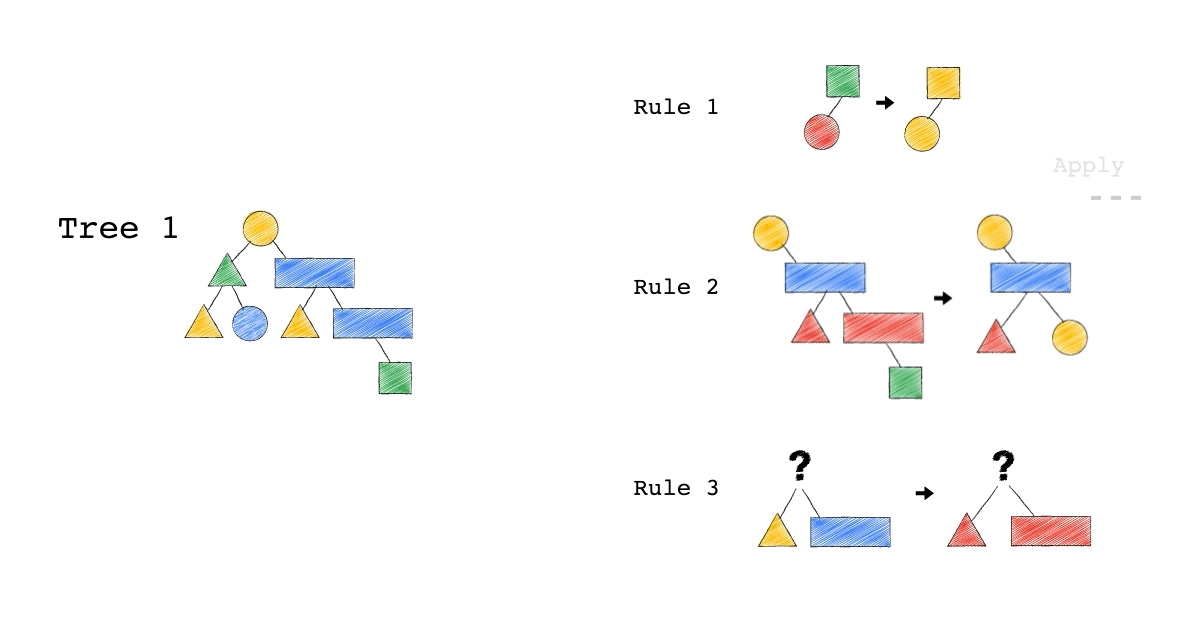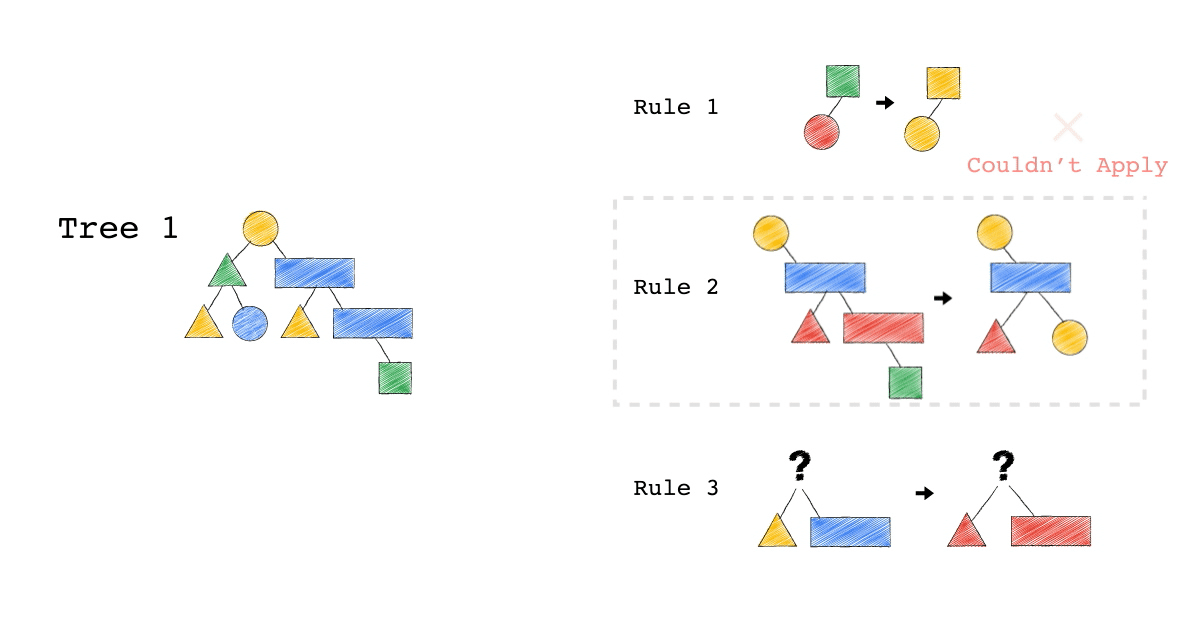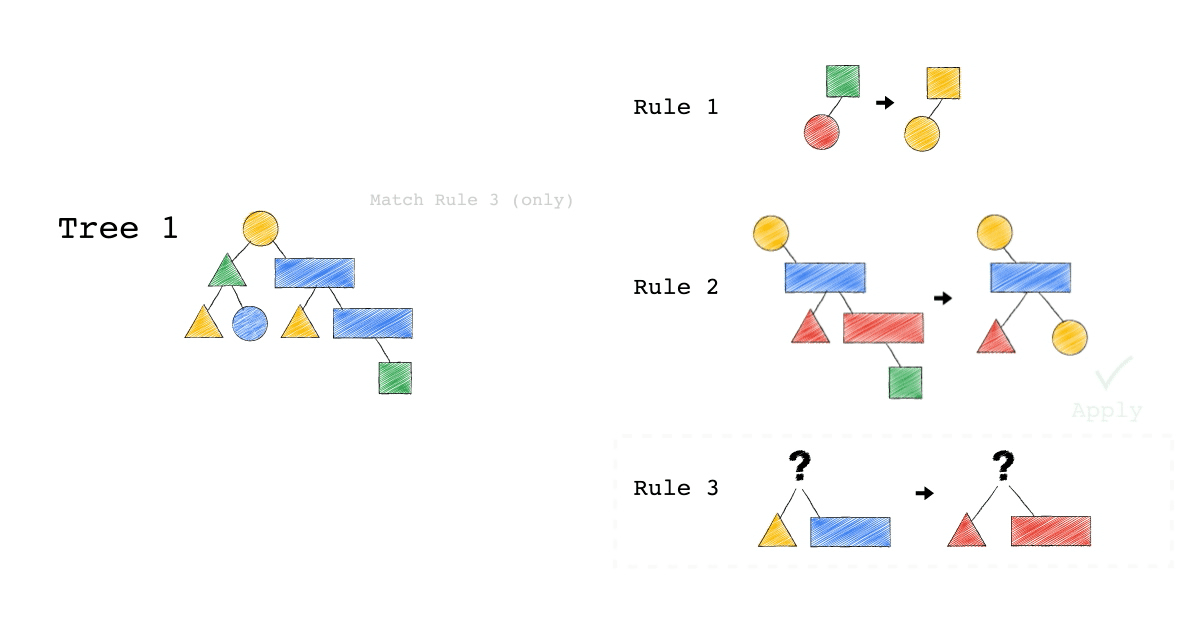
Tree1 gif

    一開始，只有一顆 Tree1 (代表著初始的 Query Plan，可以想像成，使用者寫出來的 Query)

我們一次 Apply 一個 Rule 到 Tree1 上，看看有沒有 Match 成功，如果有，就會生成一顆新的 Tree，以上圖來說 Tree 1 只 Match 到了 Rule3 ， 所以只生成了一顆 Tree2(見下圖)。

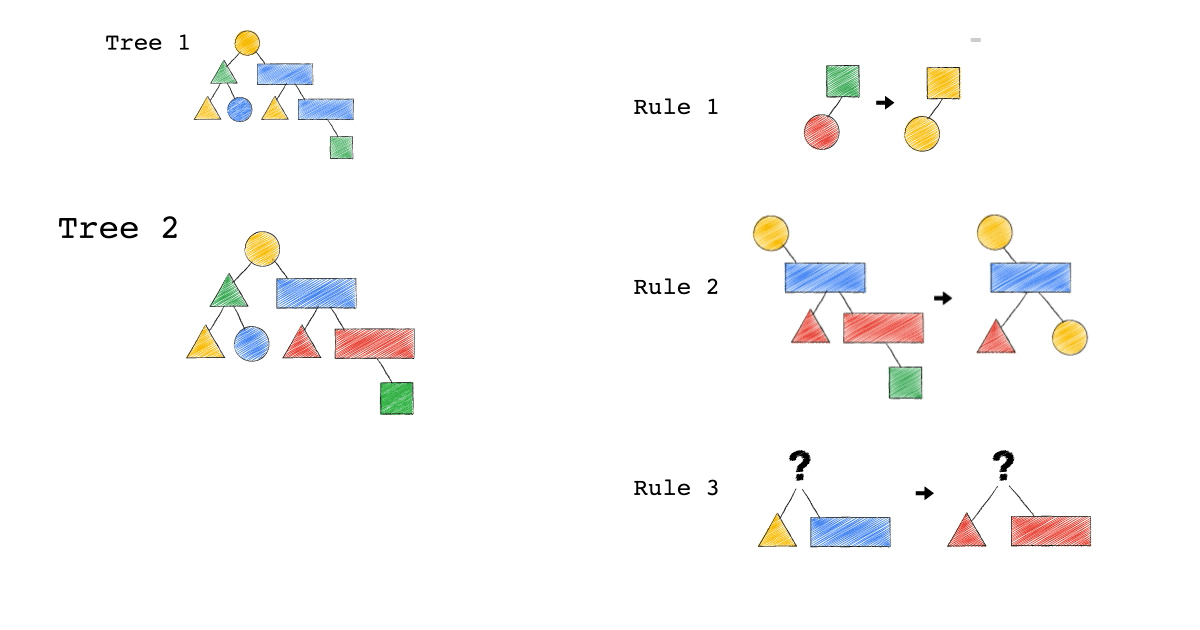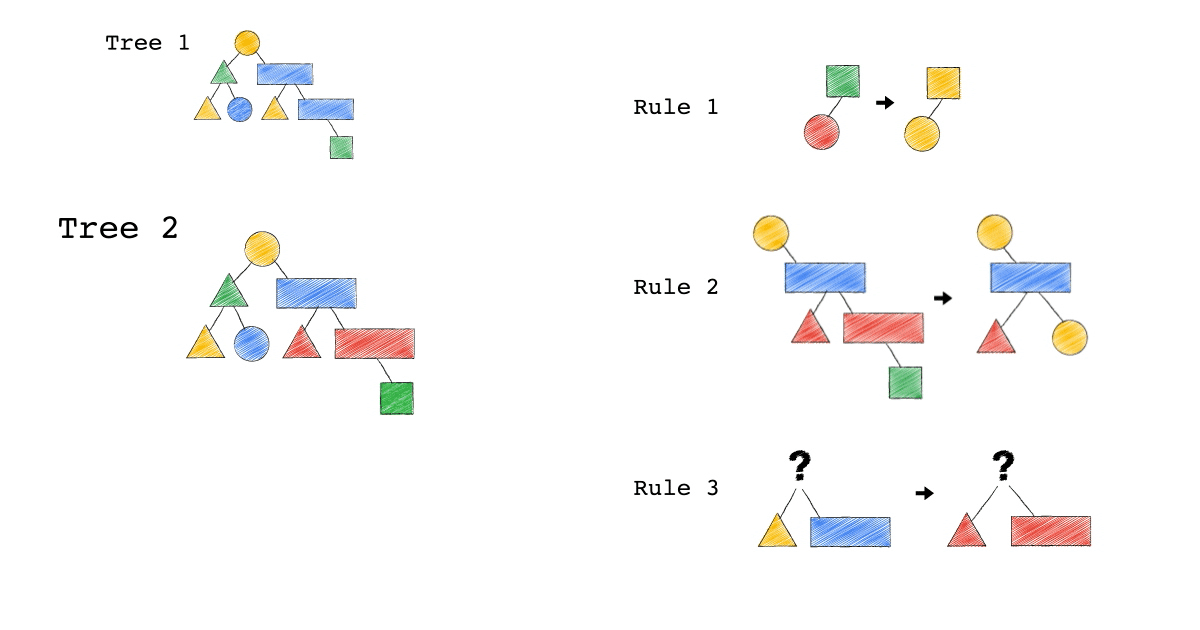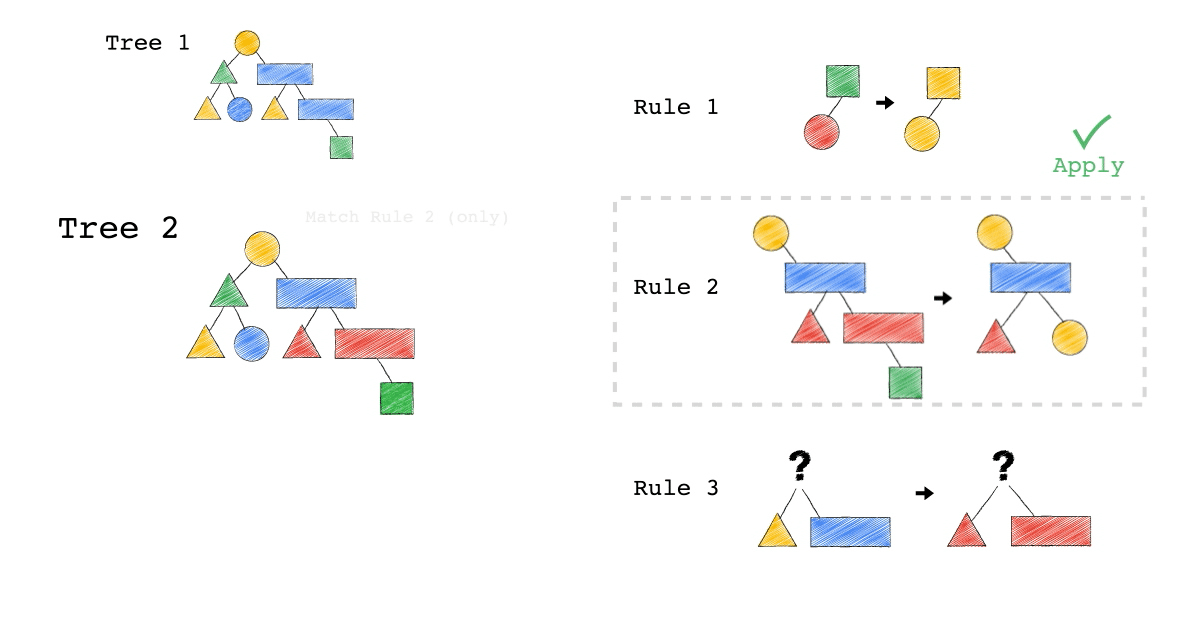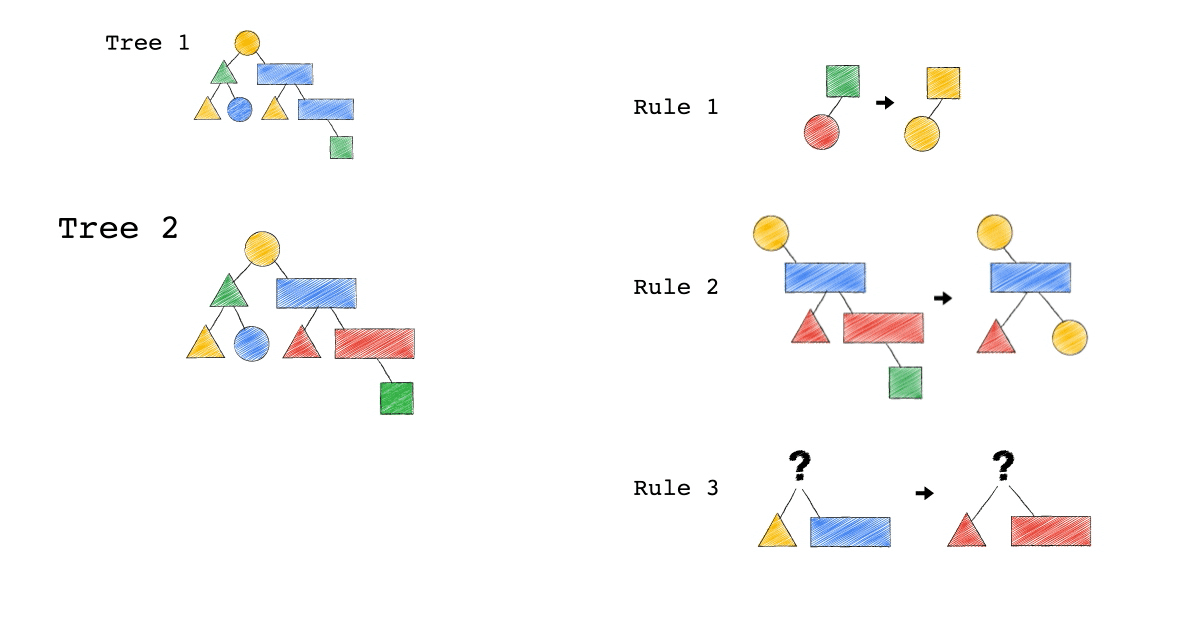
Tree2 gif

   Tree2 的生成，是因為 Tree1 Match 到的 Pattern，被 Substitute 成指定的 Pattern 了，本來 Tree1 左子節點是黃色三角形，與右子節點是藍色長方形的 Pattern，通通被換成紅色版本的(Rule 3)。

Rule 就是一個 要換掉什麼 Pattern (Match)，把該 Pattern ，換成什麼 Pattern (Substitute)，的函式。

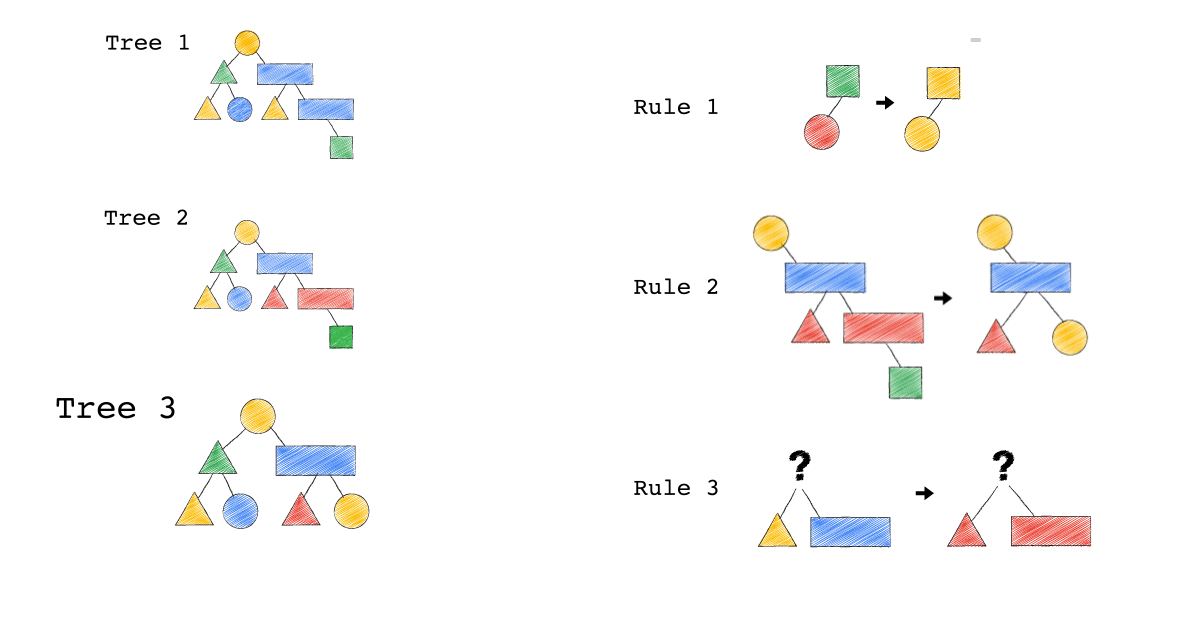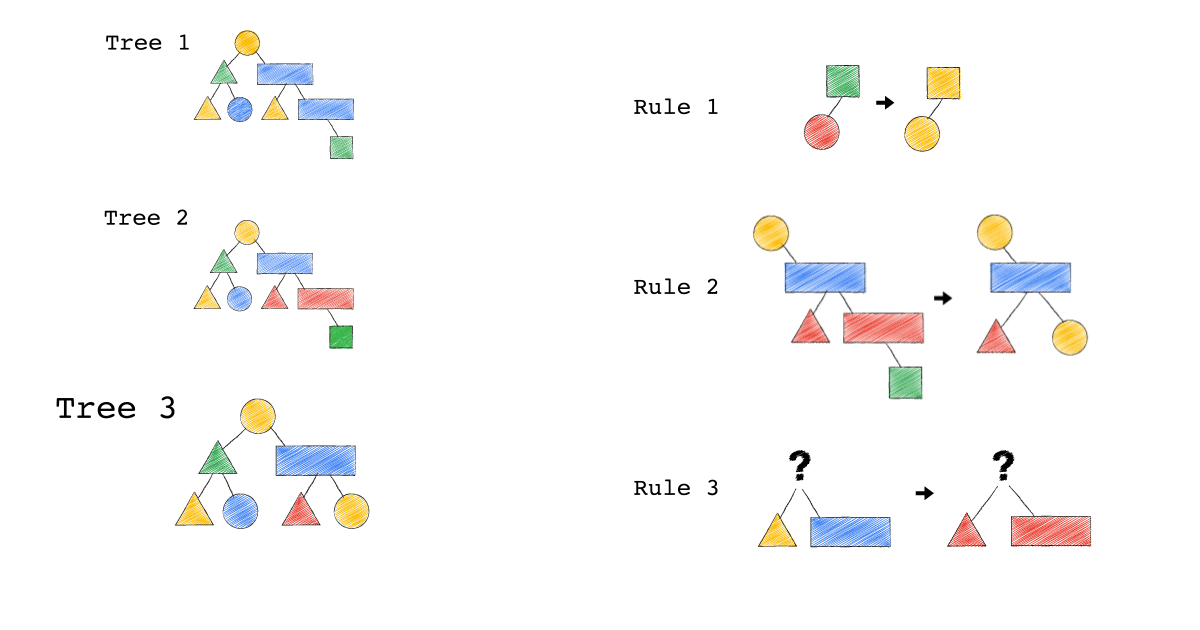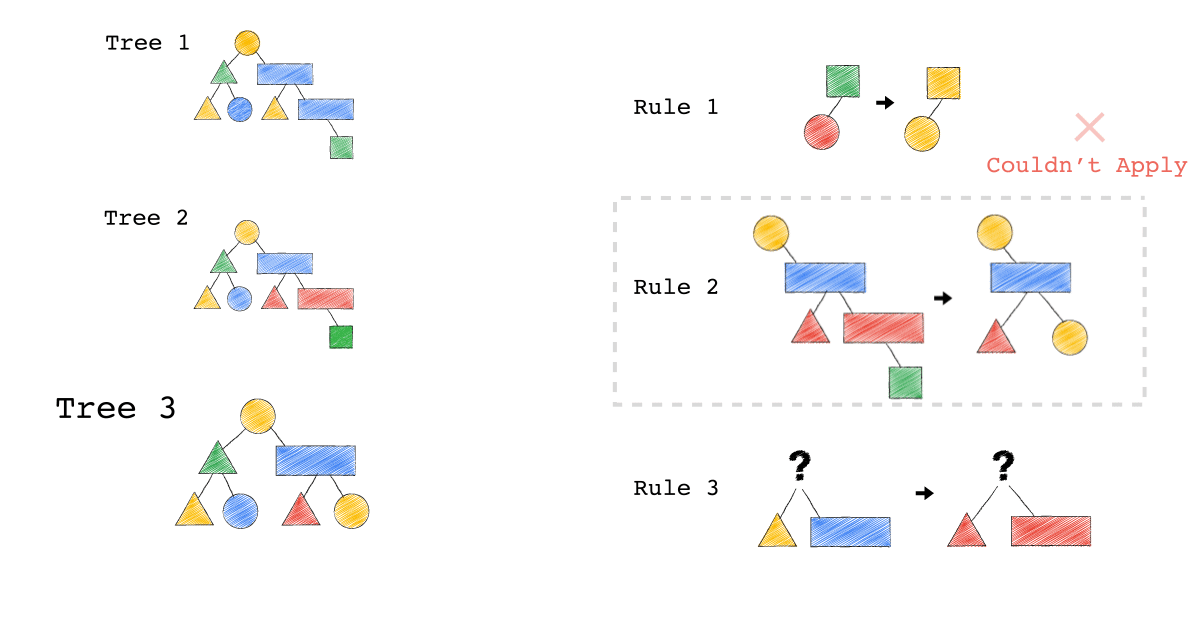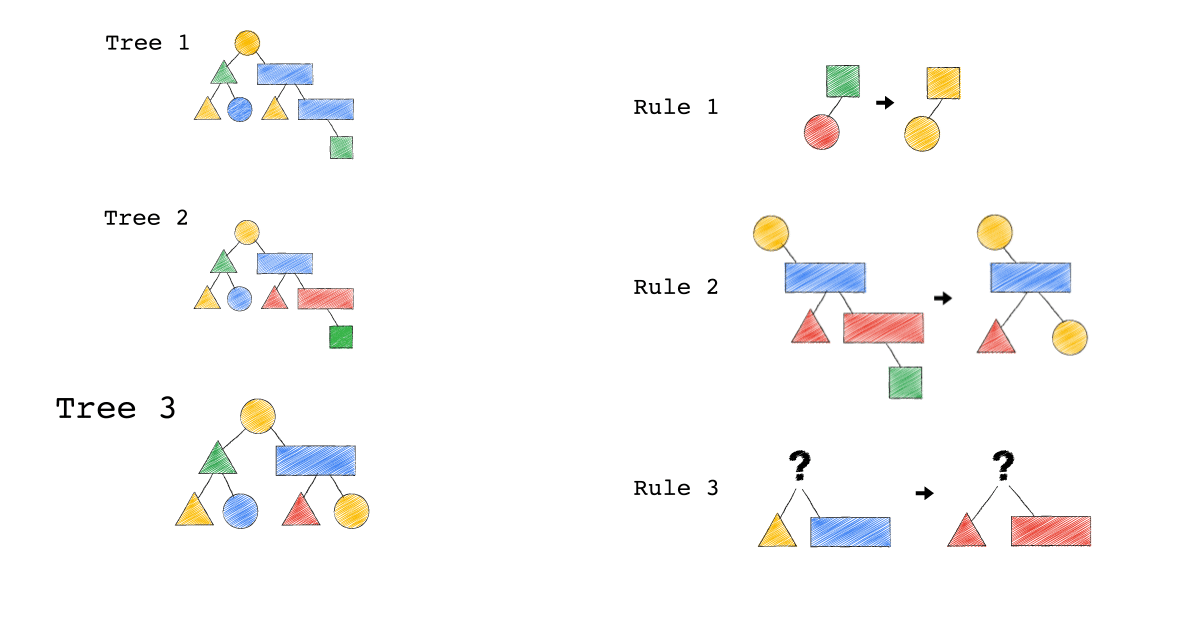
Tree3 gif

   Tree3 的生成，是因為 Tree2 成功 Match Rule 2，而 Tree3 本身則沒有再成功 Match 到任何 Rule。

你有發現一件事嗎? 本來 Tree1 不能 Apply Rule 2，但是 Tree1 生成的 Tree2 卻因為 Rule 3 的 Substitute， 竟然可以 Apply Rule 2 了。

可以再仔細看，第一張動畫，跟第二張動畫在 Rule 2 的區別。為什麼第一張 Match 失敗 Rule2，第二張卻成功了 ?

請記得這件事，Plan 本來不能 Apply RuleX，但假如先 Apply RuleY(會生成一個新的 Plan Tree)，新的 Plan Tree 竟然就可以 Apply RuleX 了。

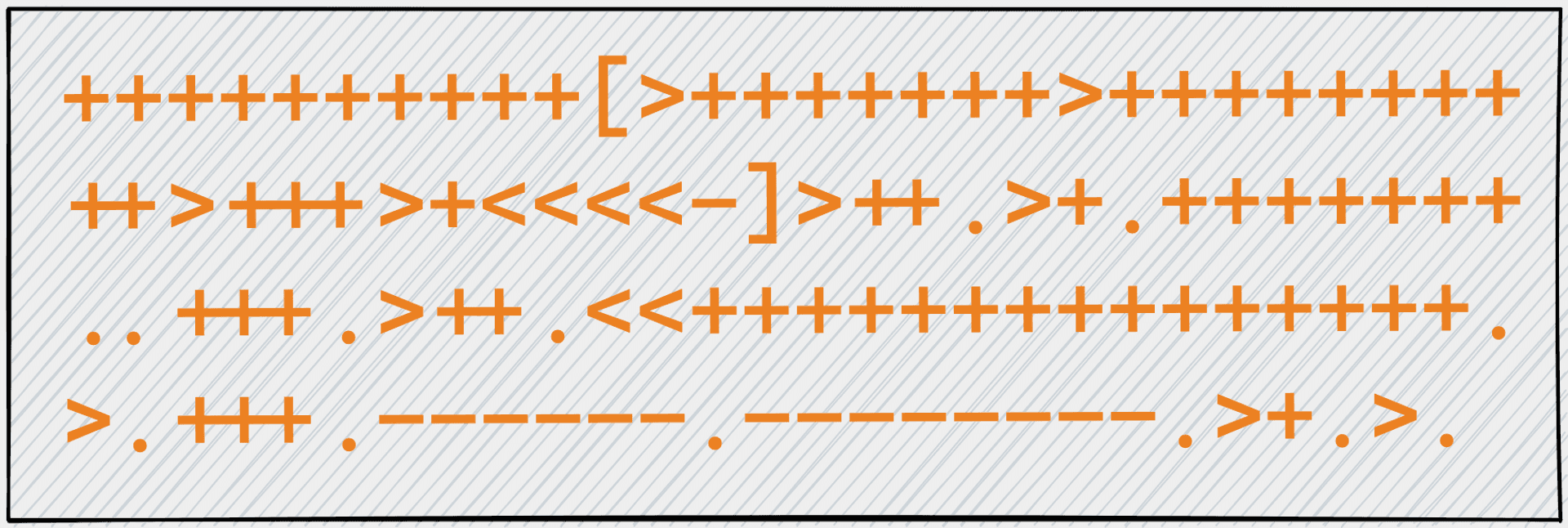
    Pattern Matching 在 Cascades 風格的優化器實作上，最大的幫助就是 Rule 。不用 Pattern Matching ，當然也是可以實作 Cascades 風格的優化器，只是 Michael Armbrust 的 Scala 火力展示，實在令人印象深刻，你很難不想用 Pattern Matching。

我的 Python 程式目前只是簡單的探索 Structural Pattern Matching 語法，還沒有利用 Structural Pattern Matching 寫出完整的 Rule，去優化某些事情。不過有一個超級棒的專案，具體而微展示了 Spark SQL (Catalyst)的優化思路。

由另一位 Spark PMC，Cheng Lian (Databricks 🧱 Engineering Manager )，所寫的小專案，透過 Spark Catalyst 的想法(Cascades)來實作一個 Brainfuck 編譯器，該專案叫做 Brainsuck。

Brainfuck 作為知名的圖靈完備語言，就跟課本上圖靈機說的一樣，用一條長長的紙帶，計算想要解決的問題。

因為 Brainfuck 精巧的只用到了 8 個指令([]<>+-.,)，也常被拿來實作有教育意義專案， Jserv 所領導的系統程式課程，虛擬機器設計與實作，正是透過打造一個 Brainfuck 的編譯器，探討編譯器的基本概念。

不管是 Cheng Lian 或是 Jserv，他們都透過進一步的實作 brainfuck optimization strategies 所提到的優化策略，改善編譯器的效能。

Cheng Lian 的 Brainsuck 想法是這樣，首先先把 Brainfuck 程式轉成一顆 IR 樹，接著把 brainfuck optimization strategies 所提到的策略，寫成 Rule 的形式，透過 Rule 去轉換 IR 樹。

Brainsuck 定義的 IR 有 10 種，摘自 Dive into Catalyst 投影片 P.23

每一個 Brainfuck 程式都會先被轉成一顆 IR 的樹，摘自 Dive into Catalyst 投影片 P.32
*這頁的 Brainfuck 程式，我覺得怪怪的，因為它會超過紙帶的範圍，但是主要要表達的意思，我認為是

Brainfuck 程式 +[<]+>. 轉成 IR 樹會長怎樣

沒錯，既然有了 IR 樹，就可以採用 Cascades 風格式的作法， 對 IR 樹一直 apply Rule，不斷轉換成執行效率更高的 IR 樹。

Brainsuck 總共有 6 個 Rules，經過不斷的轉換 IR 樹，把一個 Brainfuck 寫成的河內塔程式，加速了超過 20 倍。

舉例來說
本來需要，多個 Moves，合併成只要 1 個 Move，摘自 Dive into Catalyst 投影片 P.40

這個合併 Move 的 Rule，寫起來就是這樣的輕巧，摘自 Dive into Catalyst 投影片 P.41

Brainsuck 專案充分地展現了，Goetz Graefe 的抽象設計，有多麽強大，本來是用作 Query Optimizer 的架構，竟然也可以用在 Compiler 的優化上。只要你要優化的對象是一顆樹，你知道把樹上的某些 Pattern 轉換成另一種 Pattern，可以得到你更喜歡的樹。就可以用把轉換的過程寫成一個個獨立的 Rules，再透過 Rules 去操作樹。



    Cascades 風格的優化器，把優化器開發，聚焦成了對一個個 Rule 的開發，是真正了不起的架構。任一個工程師只需要專注在一個 Rule 上，大大降低了開發上的心智負擔。此外通過增加 Rule，優化器的擴充性非常好，對比非 Cascades 風格的優化器(後面會有 Cascades 風格 跟 Postgres 對比的例子)，更能良好的管理優化器的迭代、測試、驗證。

想要擴充 Spark SQL 的功能，就是透過新增 Rule，讓樹有可能有新的形狀，以一個真實的 Spark Issue 為例，看看 Spark 新增一個 Rule 需要做什麼事？

Spark PMC Liang-Chi Hsieh 謝良奇 (Apple  Software Engineer) 在 2021 11/12 月的 Commits，是很好的學習例子。

這個 Issue 的需求是這樣的，假如 Spark 使用者只想知道一個有多層結構的資料(JSON、Parquet...)，有多少個子元素，其實可以把沒用到的欄位丟掉，簡單摘要如下。

So is there any way how to get size of array in parquet without reading whole sub-structure? If it is not, you showed at least optimization, read the "smallest" attribute in sub-structure. And I think that is the job for optimizer, user needs just size of array. - Jiri Humpolicek

舉例來說，使用者想知道以下 items 有幾個 item ?

val jsonStr = """{
 "items": [
   {"itemId": 1, "itemData": "a"},
   {"itemId": 2, "itemData": "b"}
 ]
}"""
== Optimized Logical Plan ==
Aggregate [count(1) AS count(true)#20299L]
+- Project
   +- Generate explode(items#20293), [0], false, [item#20296]
      +- Filter ((size(items#20293, true) > 0) AND isnotnull(items#20293))
         +- Relation default.table[items#20293] parquet

Generate 這個 node，會展開整個多層結構的資料成一個 array，但其實假如只想知道，這個 array 的大小，其實不用包含所有的原始資料，或者更簡單說。使用者想要 Spark 跟 Parquet 的行為一致(詳見 Jira)。

這個 Issue 是 Spark SQL 原有的 Rules 沒辦法做優化的，所以預期可以看到，新增 1 個 Rule，在 Spark SQL 要怎麼寫？

❗❗❗ 這邊先聲明，我不會 Scala，對 Spark 的原理也一無所知，這裏我只是嘗試想理解，真實為 Cascades 風格優化器加 1 個 Rule，該怎麼做。 我有任何理解錯誤，歡迎指正我。

我認為比較這個 PR 的第一個 Commit 跟最後完整版的 PR，可以學到很多東西。

第一個 Commit，我覺得就是非常好的學習素材，因為完整的展現了，新增 1 個 Rule，在 Spark SQL 要做什麼事？

  1. 寫 Rule
  2. 注入 Rule 到 Opitimizer 中
  3. Rule 的單元測試 (其實這是在第二個 Commit 中，但算是一起完成的工作)



1. 寫 Rule #

前面第二張動畫說明提到，Rule 就是一個 要換掉什麼 Pattern (Match)，把該 Pattern ，換成什麼 Pattern (Substitute)，的函式。

這個 Commit，新加的 Rule 叫做 CountAggregateOptimization，顧名思義就是要去優化有CountAggregate 的 Plan Tree。

其中

就是在做 要換掉什麼 Pattern (Match) 這件事，要換掉的 Pattern 是 CountAggreate 的子節點，包含了一個空 Projection 連著 Generate(explode) 。

換成什麼 Pattern (Substitute)，就是把要 Explode 全部欄位，換成 Explode 一個 atomic 的欄位就好。



2. 注入 Rule 到 Opitimizer 中 #

非常簡單

在 .../catalyst/rules/RuleIdCollection.scala

加一行 "org.apache.spark.sql.catalyst.optimizer.CountAggregateOptimization" ::



3. 測試 #

測試 Rule 有沒有真的 apply



我想透過這個 PR 表達的事情是，撰寫新 Rule 時

工程師的關注點是很聚焦的，而且 Pattern Matching 讓 Rule 的撰寫很直觀。

這個 Commit 扣掉測試，只需要 69 行，不過這個 Commit 的跟最後的 PR 還有一些差距，主要的變化是 Spark PMC Wenchen Fan (Databricks 🧱 Senior Software Engineer)，指出新增加的這個 Rule 可以寫得更泛用，不用只關注在 CountAggregate，因為 ColumnPruning 這個舊 Rule，會產生空 Projection(有 CountAggregate 情況下)。

所以這個新 Rule，可以只關注，空 Projection 連著 Generate(explode) 的 Pattern。然後把這個 Pattern 的 explode 全部資料，縮減成 explode 大小最小的欄位。要 Match 的 Pattern，不需要只鎖定 Aggregate 的子節點。

最後的 PR 把

拿掉，並且換了一個更一般化 Rule 名稱，GenerateOptimization，Rule 程式碼縮小成 37 行，卻得到一個更泛用的 Rule(可以仔細觀察，第一個 Commit 跟最後的 PR，最後的 PR 完全沒有去 Match Aggregate node 了)。

從這個 PR 可以看出，雖然理論上可以單獨開發每一個 Rule，但並不完全像我前面所說的不用去理解其他的每一個 Rule ， 不用去關注新 Rule 與舊 Rules 間互動，更了解其他 Rule 會轉換出什麼形狀的樹，更有機會寫出更優雅的新 Rule。

強調一下，不關注舊 Rule，還是可以開發優化器(Cascades 風格優化器就是這麼強悍 no 🐦🐦🐦 nlnlOUO)，只是更了解舊 Rule，程式有機會寫得更好。

不過可以肯定的事情是，我們並不用關注每個 Rule 間 apply 的順序，因為前面那個 PR 完全沒有指定新 Rule 要 apply 的時機是怎麼樣。



但是 #



不關注每個 Rule 間 apply 的順序，要怎麼確定不會有死結，例如

Plan tree A apply RuleX 變成 Plan tree B
Plan tree B 又 apply RuleY 變回 Plan tree A，如此反覆循環。

更困難的事情是，假如形成死結的 rule 順序非常長，要怎麼發現?

其他人也有這種問題，可以參考

要回答這個問題，就必須討論到 MEMO 這個 Volcano 與 Cascades 中重要的森林資料結構，為什麼在 Spark 中並沒有? 但為什麼 Apache Calcite 卻有實作 MEMO ?

因為目前只介紹了 Volcano Cascades 的一半故事，但希望這一半的故事說服了你，"Everything is a tree" 這個想法。



MEMO 與 Volcano Cascades #

(待續...)



(待續...)
前面有提到的 Guy Lohman 與 Kiyoshi Ono，在後續的研究中[19]，實證了考慮整個樹空間與考慮 Cross Product，會產生較佳的 Plan tree。



推薦課程 #

基本上資料庫課程介紹到 Query Optimization，都會從 System R 開始介紹起。推薦以下課程

MIT 6.830/6.814
Sam Madden 基本上就是把[13]用版書講過一遍，算是蠻清楚的。

Berkeley CS 186
Joe Hellerstein 除了[13]，又多講了 Histogram 與[13]的假設會發生的問題。

清大 資料庫系統概論
吳尚鴻，我認為是台灣目前最清楚的講解影片，尤其是 System R 的 DP ，講的非常好，我第一次搞懂 System R 的演算法，就是看吳尚鴻教授的影片搞懂的。

CMU 15-445
2021 年是 Andy Pavlo 的指導學生 Lin Ma 和布朗大學的博士 Andrew Crotty 來上，前幾年是 Andy Pavlo 本人，除了講解[13]，還會提到很多真實業界的資料庫優化器，整個課程也很完整，除了課程內容，每週都有真實的業界或學術界的人來談他們怎麼做資料庫，你怎麼能不喜歡 Andy Pavlo。

Saarland Universit
Jens Dittrich，最全面的 Hash Join 與 Sort-Merge Join 比較之論文作者，關於[13]的演算法也講得很好。

TUM Query Optimization
Thomas Neumann，一般資料庫課程 Query Optimization 是一堂課的份量， TUM 是一學期份量的課，應該是研究 Query Optimization 最厲害的團隊。



參考資料 #

[1] https://www.linkedin.com/in/david-dewitt-30189b50/
事實上 David DeWitt 教授已經離開 UW-Madison 多年了，現在主要應該是 Splunk 的 VP，在 MIT 兼課。

[2] https://tech-blog.cymetrics.io/posts/maxchiu/turbofan/
cymetrics blog 對 V8 Turbofan 非常精彩的分析

[3] Designing Data-Intensive Applications , Martin Kleppmann

[4] MapReduce: A major step backwards
David DeWitt , Mike Stonebreaker

[5] https://twitter.com/uhoelzle/status/1177360023976067077
Urs Hölzle(Google SVP Engineering)

[6] https://twitter.com/joe_hellerstein/status/1222818679491923968

[7] https://zhuanlan.zhihu.com/p/97085692

[8] https://pola-rs.github.io/polars-book/user-guide/

[9] https://en.wikipedia.org/wiki/Fundamental_theorem_of_software_engineering

[10] Predicate Migration: Optimizing Queries with Expensive Predicates
SIGMOD, 1993

[11] How Good Are Query Optimizers, Really?
VLDB, 2015

[12] SQL Query Optimization. Why is it so hard to get right?
David DeWitt

[13] Access Path Selection in a Relational Database Management System
SIGMOD, 1979

[14] Explaining the Postgres Query Optimizer
Bruce Momjian

[15] PostgreSQL Optimizer Methodology
Robert Haas

[16] Understanding Cost Models
Justin Jaffray

[17] Is Query Optimization a “Solved” Problem?
Guy Lohman

[18] Analyzing Plan Diagrams of Database Query Optimizers
VLDB, 2005

[19] Measuring the Complexity of Join Enumeration in Query Optimization
VLDB, 1990

[20] An Overview of Query Optimization in Relational Systems
PODS, 1998

[21] David DeWitt Speaks Out
SIGMOD, 2002

[22] Pat Selinger Speaks Out
SIGMOD, 2003

[23] The EXODUS Optimizer Generator
SIGMOD, 1987

[24] The Volcano Optimizer Generator: Extensibility and Efficient Search
ICDE, 1993

[25] The Cascades Framework for Query Optimization
IEEE Data Engineering Bulletin, 1995

🙏🙏🙏

感謝你讀到最後, 如果你覺得這篇文章讓你有收穫， 趕快分享給你的朋友R~~ 💖! 如果有什麼想問我， 歡迎寫信給我 。